辽宁省锦州市太和区2021-2022学年七年级上学期期中数学试题
试卷更新日期:2022-09-16 类型:期中考试
一、单选题
-
1. 下列几何体中,面的个数最多的是( )A、
 B、
B、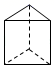 C、
C、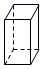 D、
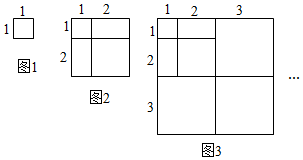
D、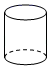 2. 已知图1的小正方形和图2中所有的小正方形都全等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是不能围成一个正方体的.那么安放的位置是( )
2. 已知图1的小正方形和图2中所有的小正方形都全等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是不能围成一个正方体的.那么安放的位置是( ) A、① B、② C、③ D、④3. 在数 , ﹣1, , , 0中,负分数有( )A、1个 B、2个 C、3个 D、4个4. ﹣2022的相反数是( )A、﹣2022 B、2022 C、±2022 D、20215. 下列算式正确的是( )A、0-(-3)=-3 B、-5+(-5)= 0 C、 D、-5-(-3)= -86. 下列代数式符合书写要求的是( )A、7 xy B、ab×9 C、 D、1÷a7. 下列各式中,与 为同类项的是( )A、 B、 C、 D、8. 下列计算结果相等的为( )A、23和32 B、﹣23和|﹣2|3 C、﹣32和(﹣3)2 D、(﹣1)2和(﹣1)4
A、① B、② C、③ D、④3. 在数 , ﹣1, , , 0中,负分数有( )A、1个 B、2个 C、3个 D、4个4. ﹣2022的相反数是( )A、﹣2022 B、2022 C、±2022 D、20215. 下列算式正确的是( )A、0-(-3)=-3 B、-5+(-5)= 0 C、 D、-5-(-3)= -86. 下列代数式符合书写要求的是( )A、7 xy B、ab×9 C、 D、1÷a7. 下列各式中,与 为同类项的是( )A、 B、 C、 D、8. 下列计算结果相等的为( )A、23和32 B、﹣23和|﹣2|3 C、﹣32和(﹣3)2 D、(﹣1)2和(﹣1)4二、填空题
-
9. 用一个平面去截正方体,边数最多的截面是边形.10. 绝对值不大于10的所有整数的和等于.11. 近年来,国家重视精准脱贫,收效显著.目前,在现行标准下,约98990000农村人口全部脱贫98990000这个数用科学记数法应表示为 .12. 计算﹣100÷5× =.13. 已知单项式的系数是 , 次数是 , 则 .14. 已知|x﹣1|+|y+2|=0,则2x﹣y= .15. 如图.将面积为a2的小正方形与面积为b2的大正方形放在一起(a>0,b>0)则三角形ABC的面积是
 16.
16.如图所示,下列各三角形中的三个数之间均具有相同的规律,根据此规律,最后一个三角形中y与n之间的关系式是 .

三、解答题
-
17. 如图,是由一些大小相同的小正方体组合成的简单几何体.
 (1)、请在下面方格纸中分别画出它的左视图和俯视图;(2)、图中共有个小正方体.18. 计算:(1)、(﹣5)+(﹣4)﹣(+101)﹣(﹣9);(2)、(﹣1)+(﹣6)+(﹣2.25)+;(3)、()×(﹣60);(4)、 .19. 化简下列各式:(1)、﹣3(2x﹣3)+7x+8;(2)、3(x2﹣y2)﹣(4x2﹣3y2);(3)、3x﹣[5x﹣(x﹣4)];(4)、3b﹣2c﹣[﹣4a﹣(c﹣3b)]+c.20. 先化简,再求值:(1)、2(a2+3a﹣2)﹣3(2a+2),其中a=﹣3;(2)、3x2y﹣[2xy﹣(2xy﹣x2y)]﹣xy的值,其中x=﹣2,y=﹣1.21. 快递员骑车从快递公司出发,先向北骑行到达小区,继续向北骑行到达小区,然后向南骑行到达小区,最后回到快递公司.(1)、以快递公司为原点,以向南方向为正方向,用表示画出数轴,并在该数轴上表示出 三个小区的位置;(2)、小区离小区有多远;(3)、快递员一共骑行了多少干米?22. 某粮仓原有大米132吨,某一周该粮仓大米的进出情况如下表:(当天运进大米8 吨,记作+8吨;当天运出大米15吨,记作﹣15吨.)
(1)、请在下面方格纸中分别画出它的左视图和俯视图;(2)、图中共有个小正方体.18. 计算:(1)、(﹣5)+(﹣4)﹣(+101)﹣(﹣9);(2)、(﹣1)+(﹣6)+(﹣2.25)+;(3)、()×(﹣60);(4)、 .19. 化简下列各式:(1)、﹣3(2x﹣3)+7x+8;(2)、3(x2﹣y2)﹣(4x2﹣3y2);(3)、3x﹣[5x﹣(x﹣4)];(4)、3b﹣2c﹣[﹣4a﹣(c﹣3b)]+c.20. 先化简,再求值:(1)、2(a2+3a﹣2)﹣3(2a+2),其中a=﹣3;(2)、3x2y﹣[2xy﹣(2xy﹣x2y)]﹣xy的值,其中x=﹣2,y=﹣1.21. 快递员骑车从快递公司出发,先向北骑行到达小区,继续向北骑行到达小区,然后向南骑行到达小区,最后回到快递公司.(1)、以快递公司为原点,以向南方向为正方向,用表示画出数轴,并在该数轴上表示出 三个小区的位置;(2)、小区离小区有多远;(3)、快递员一共骑行了多少干米?22. 某粮仓原有大米132吨,某一周该粮仓大米的进出情况如下表:(当天运进大米8 吨,记作+8吨;当天运出大米15吨,记作﹣15吨.)某粮仓大米一周进出情况表(单位:吨)
星期一
星期二
星期三
星期四
星期五
星期六
星期日
﹣32
+26
﹣23
﹣16
m
+42
﹣21
(1)、若经过这一周,该粮仓存有大米88吨,求m的值,并说明星期五该粮仓是运进还是运出大米,运进或运出大米多少吨?(2)、若大米进出库的装卸费用为每吨15元,求这一周该粮仓需要支付的装卸总费用.