吉林省吉林市永吉县2021-2022学年七年级上学期期中考试数学试题

试卷更新日期：2022-09-16 类型：期中考试

进入出卷网下载

一、单选题

1. 某年我国的商品进出口总额比上年的变化情况是增长7.5%，记作＋7.5%，而美国的商品进出口总额比上年的变化情况是减少6.4%，则可记作（）

A、－7.5% B、＋7.5% C、－6.4% D、＋6.4%

查看试题解析
2. 化简 $- (- 1)$ 的结果为（）

A、－1 B、0 C、1 D、2

查看试题解析
3. 如图，检测5个排球，其中质量超过标准的克数记为正数，不足的克数记为负数，从轻重的角度看，最接近标准的是（）

A、 B、 C、 D、

查看试题解析
4. 式子 $- 2^{3}$ 的意义是（）

A、－（2＋2＋2） B、－（2×3） C、－（3×3） D、－（2×2×2）

查看试题解析
5. 若 $2 a^{4} b + a^{m} b^{2}$ 是五次多项式，则指数m的值不可能是（）

A、4 B、3 C、2 D、1

查看试题解析
6. 有理数a，b在数轴上表示如下，则下列结论错误的是（）

A、 $b + a < 0$ B、 $b - a < 0$ C、 $a b < 0$ D、 $\frac{a}{b} < 0$

查看试题解析

二、填空题

7. 在月球表面，白天，阳光垂直照射的地方，温度高达零上127℃；夜间，温度可降至零下183℃；则在月球表面的昼夜温差是．

查看试题解析
8. 比较大小： $- \frac{8}{21}$ $- \frac{3}{7}$

查看试题解析
9. 神舟十二号在二零二一年六月十七号上午九点二十二分火箭点火十分钟后，飞船成功进入距离地球最近点约200000千米的预定轨道，发射任务圆满完成，数据200000用科学记数法表示为．

查看试题解析
10. 小明同学买5本笔记本，用了m元，用式子表示：若买相同的笔记本8本，则付钱元．

查看试题解析
11. 已知有理数m，n是互为相反数，且a，b是互为倒数，则式子 $\frac{2 m + 2 n - 3 a b}{2021}$ 的值为．

查看试题解析
12. 在东京奥运会上的男子百米半决赛小组比赛中，我国名将苏炳添和美国选手贝克尔（音译）的成绩都是9.83s，但是裁判最后判定我国名将苏炳添排名小组第一，美国选手排名小组第二，则两人的成绩至少都精确到了位，才可能分出名次的．

查看试题解析
13. 已知： $2 x^{3 - m} y^{n + 2}$ 和 $- x y^{3}$ 是同类项，则m+n的值＝．

查看试题解析
14. 测得一种树苗的高度（h）与树苗生长（n）的年数的有关数据如下表：
年数（n）
高度（h）/cm
1
100＋5
2
100＋10
3
100＋15
4
100＋20
……
……
假设以后各年树苗的变化与年数保持上述关系，用式子表示生长了n年的树苗高度h，则h＝（用含n的式子表示）．

查看试题解析

三、解答题

15. 计算： $(- 3 \frac{3}{4}) \div (- 1 \frac{1}{2}) \times (- \frac{2}{5})$ ．

查看试题解析
16. 计算： $(- 20) + (+ 3) - (- 5) + (- 7)$ ．

查看试题解析
17. 计算： $42 \times (- \frac{2}{3}) + (- \frac{3}{4}) \div (- 0.25)$ ．

查看试题解析
18. 计算： $- (3 - 5) + 3^{2} \times 2 \div (- 1)^{3}$ ．

查看试题解析
19.

(1)、在数轴上表示下列各数：0，2，－0.5，－3．

(2)、把（1）中的数用“＜”号连接起来．

查看试题解析
20. 将下列各数中的负数、整数和负分数分别填入对应的集合内：
－2，0，＋1， $- \frac{3}{5}$ ， 3．
负数集合：{                     ……}；
整数集合：{             ……}；
负分数集合：{        ……}．

查看试题解析
21. 某同学化简 $\frac{1}{2} x - 2 (x - \frac{1}{3} y^{2}) + (- \frac{3}{2} x + \frac{1}{3} y^{2})$ 出现了不符合题意，解答过程如下：
原式＝ $\frac{1}{2} x - (2 x - \frac{2}{3} y^{2}) + (- \frac{3}{2} x + \frac{1}{3} y^{2})$         （第一步）
＝ $\frac{1}{2} x - 2 x - \frac{2}{3} y^{2} - \frac{3}{2} x + \frac{1}{3} y^{2}$                  （第二步）
＝ $- 3 x - \frac{1}{3} y^{2}$ ．                                         （第三步）

(1)、该同学解答过程从第步开始出错，错误原因是；

(2)、写出正确的解答过程．

查看试题解析
22. 一种商品每件成本a元，原来按成本增加20%定出价格，现在由于库存积压减价，按原售价的90%出售．

(1)、求现在每件商品还能盈利多少元？（用含a的式子表示）

(2)、若a＝150元，则现在每件商品还能盈利元．

查看试题解析
23. 先化简，再求值：
$5 (3 a^{2} b - a b^{2}) - (a b^{2} - 3 a^{2} b) + (3 a b^{2} - 6 a^{2} b)$ ，其中 $a = - \frac{1}{2}$ ， $b = \frac{2}{3}$ ．

查看试题解析
24. 如图，池塘边有一块长为20m，宽为10m的长方形土地，现在将其余三面留出宽都是xm的小路，中间余下的长方形部分做菜地．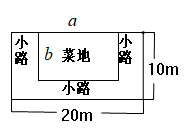

(1)、菜地的长a＝m，菜地的宽b＝m（用含x的式子表示）；

(2)、如果要将菜地周围围上栅栏（靠水池的一边不用围）．
①求所用栅栏的总长度l（用含x的式子表示）；
②当x＝1时，求栅栏的总长度l为多少米？

查看试题解析
25. 做大小两个长方体纸盒，尺寸如下（单位：cm）：

长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c

(1)、1个小纸盒的表面积是cm² ， 1个大纸盒的表面积是cm²（用含a，b，c的式子表示）；

(2)、求做这样的2个小纸盒和1个大纸盒共用料多少平方厘米？（用含a，b，c的式子表示）

(3)、求做这样的1个大纸盒比做这样的1个小纸盒多用料多少平方厘米？（用含a，b，c的式子表示）

查看试题解析
26. 某自行车厂一周计划生产1050辆自行车，平均每天生产150辆，由于各种原因实际每天生产的情况如下（超产记为正，减产记为负）：
星期
一
二
三
四
五
六
日
增减
＋5
－2
－4
＋13
－10
＋16
－9

(1)、根据记录可知前三天生产自行车辆；

(2)、产量最多的一天比产量最少的一天多生产辆；

(3)、这一周实际生产自行车多少辆？超产还是减产多少辆？

查看试题解析

年数（n）	高度（h）/cm
1	100＋5
2	100＋10
3	100＋15
4	100＋20
……	……

星期	一	二	三	四	五	六	日
增减	＋5	－2	－4	＋13	－10	＋16	－9

	长	宽	高
小纸盒	a	b	c
大纸盒	1.5a	2b	2c