吉林省吉林市船营区2021-2022学年七年级上学期期中数学试题
试卷更新日期:2022-09-16 类型:期中考试
一、单选题
-
1. 若运算“1□(﹣2)”的结果为正数,则□内的运算符号为( )A、+ B、﹣ C、× D、÷2. 2021年2月25日,全国脱贫攻坚总结表彰大会顺利召开,标志着我国脱贫攻坚战取得了全面胜利,现行标准下98990000农村贫困人口全部脱贫,创造了又一个彪炳史册的人间奇迹,数据98990000用科学记数法表示为( )A、 B、 C、 D、3. 下列各式中,不相等的是( )A、 和 B、 和 C、 和 D、 和4. 若4anb3与﹣3a5bm﹣1是同类项,则m﹣n=( )A、﹣1 B、1 C、﹣2 D、25. 已知 , ,则 的值是( )A、-1 B、1 C、-5 D、156. 《增删算法统宗》记载:“有个学生资性好,一部孟子三日了,每日增添一倍多,问若每日读多少?”其大意是:有个学生天资聪慧,三天读完一部《孟子》,每天阅读的字数是前一天的两倍,问他每天各读多少个字?已知《孟子》一书共有34 685个字,设他第一天读x个字,则下面所列方程正确的是( ).A、x+2x+4x=34 685 B、x+2x+3x=34 685 C、x+2x+2x=34 685 D、x+ x+ x=34 685
二、填空题
-
7. 比较大小:﹣ (填“>”或“<”).8. 比小的数是 .9. 已知单项式的系数是 , 次数是 , 则 .10. 如图,在数轴上,注明了四段范围,若某段内有两个整数,则这段是 .
 11. 已知: , 且 , 则的值是 .12. 买一个篮球需要m元,买一个足球需要n元,那么买4个篮球和7个足球共需元.13. 如果 , 那么14. 用火柴棍按如图所示的方式摆大小不同的“E”,依此规律,摆出第个“E”需要火柴的根数是
11. 已知: , 且 , 则的值是 .12. 买一个篮球需要m元,买一个足球需要n元,那么买4个篮球和7个足球共需元.13. 如果 , 那么14. 用火柴棍按如图所示的方式摆大小不同的“E”,依此规律,摆出第个“E”需要火柴的根数是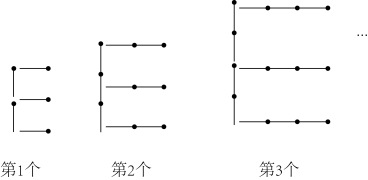
三、解答题
-
15. .16.17. 先化简再求值:2(a2+3a﹣2)﹣3(2a+2),其中a=﹣3.18. 解方程:3x+2(x﹣2)=6.19. 下面是小彬同学解一元一次方程的过程,请认真阅读并完成相应任务.
解方程: .
解:( ),得 . ……第一步
去括号,得 . ……第二步
移项,得 . ……第三步
合并同类项,得 . ……第四步
方程两边同除以2,得 . ……第五步
填空:
(1)、以上求解步骤中,第一步进行的是 , 这一步的依据是;(2)、以上求解步骤中,第步开始出现错误,具体的错误是;(3)、该方程正确的解为 .20. 有8筐白菜,以每筐25千克为标准,超过的千克数记作正数,不足的千克数记作负数,称后的纪录如下:

回答下列问题:
(1)、这8筐白菜中最接近标准重量的这筐白菜重千克;(2)、与标准重量比较,8筐白菜总计超过或不足多少千克?(3)、若白菜每千克售价2.6元,则出售这8筐白菜可卖多少元?21. 如图,约定:上方相邻两整式之和等于这两个整式下方箭头共同指向的整式.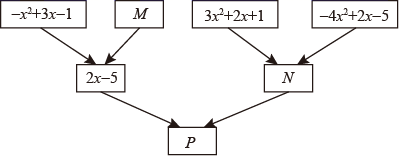 (1)、求整式 .(2)、先求整式 ,再自选一个喜欢的 值代入求出 值.22. 如图所示是一个长方形.
(1)、求整式 .(2)、先求整式 ,再自选一个喜欢的 值代入求出 值.22. 如图所示是一个长方形. (1)、根据图中尺寸大小,用含x的代数式表示阴影部分的面积 ;(2)、若x=3,求S的值.23. 如图,在一条数轴上,点O为原点,点A、B、C表示的数分别是m+1,2﹣m,9﹣4m.
(1)、根据图中尺寸大小,用含x的代数式表示阴影部分的面积 ;(2)、若x=3,求S的值.23. 如图,在一条数轴上,点O为原点,点A、B、C表示的数分别是m+1,2﹣m,9﹣4m. (1)、求AC的长;(用含m的代数式表示)(2)、若AB=5,求BC的长.24. 某中学组织一批学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆300元,60座客车租金为每辆400元,问:(1)、这批学生的人数是多少?原计划租用多少辆45座客车?(2)、若租用同一种车,要使每位学生都有座位,应该怎样租用才合算?25. 请阅读以下步骤,完成问题:
(1)、求AC的长;(用含m的代数式表示)(2)、若AB=5,求BC的长.24. 某中学组织一批学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆300元,60座客车租金为每辆400元,问:(1)、这批学生的人数是多少?原计划租用多少辆45座客车?(2)、若租用同一种车,要使每位学生都有座位,应该怎样租用才合算?25. 请阅读以下步骤,完成问题:①任意写一个三位数,百位数字比个位数字大2;
②交换百位数字与个位数字,得到一个三位数;
③用上述的较大的三位数减去较小的三位数,所得的差为三位数;
④交换这个差的百位数字与个位数字又得到一个三位数;
⑤把③④中的两个三位数相加,得到最后结果.
问题:
(1)、③中的三位数是; ④中的三位数是;⑤中的结果是;(2)、换一个数试试看,所得结果是否一样?如果一样,设这个三位数的百位数字为、十位数字为 , 用代数式表示这个三位数,并结合你所学的知识解释其中的原因.26. (阅读理解)甲、乙两人分别从A,B两地同时出发,甲骑自行车,乙骑摩托车,沿同一条路线相向匀速行驶,出发后经过0.4小时相遇,已知在相遇时乙比甲多行驶了14.4千米,相遇后经0.1小时乙到达A地.问甲、乙两人的速度分别是多少?分析可以用示意图来分析本题中的数量关系.
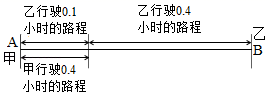
从图中可得如下的相等关系,
甲行驶0.4小时的路程=乙行驶0.1小时路程,
甲行驶0.4小时的路程+14.4=乙行驶0.4小时的路程.
根据这两个相等关系,可得到甲、乙速度的关系,设元列出方程.
(1)、(问题解决)请你列方程解答(阅读理解)中的问题.(2)、(能力提升)对于上题,若乙出发0.2小时后行驶速度减少10千米/小时,问甲出发后经多少小时两人相距2千米?