2022年秋季浙教版数学九年级上册第一章《二次函数》单元测试B
试卷更新日期:2022-09-15 类型:单元试卷
一、单选题(每题3分,共30分)
-
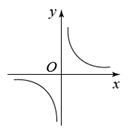
1. 抛物线的顶点坐标是( )A、 B、 C、 D、2. 已知二次函数(为常数,),点是该函数图象上一点,当时, , 则的取值范围是( )A、或 B、 C、或 D、3. 已知反比例函数 的图象如图所示,则一次函数 和二次函数 在同一平面直角坐标系中的图象可能是( )
 A、
A、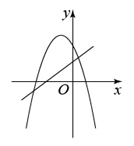 B、
B、 C、
C、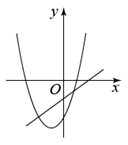 D、
D、 4. 若抛物线 与x轴两个交点间的距离为4.对称轴为 ,P为这条抛物线的顶点,则点P关于x轴的对称点的坐标是( )A、 B、 C、 D、5. 已知二次函数y=2x2−4x−1在0≤x≤a时,y取得的最大值为15,则a的值为( )A、1 B、2 C、3 D、46. 如图,抛物线的对称轴为 , 下列结论正确的是( )
4. 若抛物线 与x轴两个交点间的距离为4.对称轴为 ,P为这条抛物线的顶点,则点P关于x轴的对称点的坐标是( )A、 B、 C、 D、5. 已知二次函数y=2x2−4x−1在0≤x≤a时,y取得的最大值为15,则a的值为( )A、1 B、2 C、3 D、46. 如图,抛物线的对称轴为 , 下列结论正确的是( )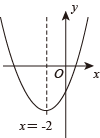 A、 B、 C、当时,y随x的增大而减小 D、当时,y随x的增大而减小7. 已知抛物线(a,b,c是常数,)经过点 , 有下列结论:
A、 B、 C、当时,y随x的增大而减小 D、当时,y随x的增大而减小7. 已知抛物线(a,b,c是常数,)经过点 , 有下列结论:①;
②当时,y随x的增大而增大;
③关于x的方程有两个不相等的实数根.
其中,正确结论的个数是( )
A、0 B、1 C、2 D、38. 如图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )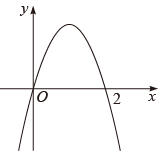 A、b>0 B、a+b>0 C、x=2是关于x的方程ax2+bx=0(a≠0)的一个根 D、点(x1 , y1),(x2 , y2)在二次函数的图象上,当x1>x2>2时,y2<y1<09. 已知抛物线 , 当时,;当时,.下列判断:
A、b>0 B、a+b>0 C、x=2是关于x的方程ax2+bx=0(a≠0)的一个根 D、点(x1 , y1),(x2 , y2)在二次函数的图象上,当x1>x2>2时,y2<y1<09. 已知抛物线 , 当时,;当时,.下列判断:①;②若 , 则;③已知点 , 在抛物线上,当时,;④若方程的两实数根为 , , 则.
其中正确的有( )个.
A、1 B、2 C、3 D、410. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为 , 且经过点(-1,0).下列结论:①3a+b=0;②若点 , (3,y2)是抛物线上的两点,则y1<y2;③10b-3c=0;④若y≤c,则0≤x≤3.其中正确的有( )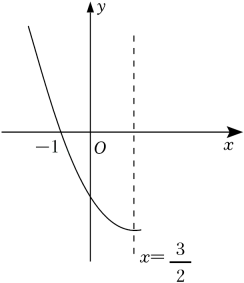 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共18分)
-
11. 已知二次函数y=﹣x2+4x+5及一次函数y=﹣x+b,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新图象(如图所示),当直线y=﹣x+b与新图象有4个交点时,b的取值范围是 .
 12. 已知y是x的二次函数,如表给出了y与x的几对对应值:
12. 已知y是x的二次函数,如表给出了y与x的几对对应值:x
…
﹣2
﹣1
0
1
2
3
4
…
y
…
11
a
3
2
3
6
11
…
由此判断,表中a=.
13. 如图,用一段长为的篱芭围成一个一边靠墙的矩形围栏(墙足够长),则这个围栏的最大面积为.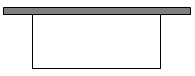 14. 规定:两个函数 , 的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数 与 的图象关于y轴对称,则这两个函数互为“Y函数”.若函数 (k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为.15. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)
14. 规定:两个函数 , 的图象关于y轴对称,则称这两个函数互为“Y函数”.例如:函数 与 的图象关于y轴对称,则这两个函数互为“Y函数”.若函数 (k为常数)的“Y函数”图象与x轴只有一个交点,则其“Y函数”的解析式为.15. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)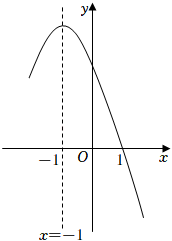 16. 如图,抛物线与x轴交于点和点 , 以下结论:
16. 如图,抛物线与x轴交于点和点 , 以下结论:①;②;③;④当时,y随x的增大而减小.其中正确的结论有 . (填写代表正确结论的序号)

三、解答题(共8题,共72分)
-
17. 丹东是我国的边境城市,拥有丰富的旅游资源.某景区研发一款纪念品,每件成本为30元,投放景区内进行销售,规定销售单价不低于成本且不高于54元,销售一段时间调研发现,每天的销售数量y(件)与销售单价x(元/件)满足一次函数关系,部分数据如下表所示:
销售单价x(元/件)
…
35
40
45
…
每天销售数量y(件)
…
90
80
70
…
(1)、直接写出y与x的函数关系式;(2)、若每天销售所得利润为1200元,那么销售单价应定为多少元?(3)、当销售单价为多少元时,每天获利最大?最大利润是多少元?18. 定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n阶方点”.例如,点是函数图像的“阶方点”;点是函数图像的“2阶方点”.(1)、在①;②;③三点中,是反比例函数图像的“1阶方点”的有(填序号);(2)、若y关于x的一次函数图像的“2阶方点”有且只有一个,求a的值;(3)、若y关于x的二次函数图像的“n阶方点”一定存在,请直接写出n的取值范围.19. 如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).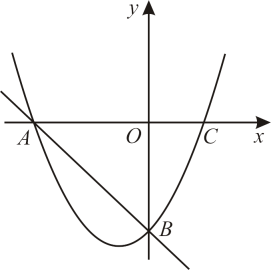 (1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.20. 如图,在平面直角坐标系中,已知抛物线的顶点为A,与y轴交于点C,线段轴,交该抛物线于另一点B.
(1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.20. 如图,在平面直角坐标系中,已知抛物线的顶点为A,与y轴交于点C,线段轴,交该抛物线于另一点B. (1)、求点B的坐标及直线的解析式:(2)、当二次函数的自变量x满足时,此函数的最大值为p,最小值为q,且.求m的值:(3)、平移抛物线 , 使其顶点始终在直线上移动,当平移后的抛物线与射线BA只有一个公共点时,设此时抛物线的顶点的横坐标为n,请直接写出n的取值范围.21. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,点B的坐标是 , 顶点C的坐标是 , M是抛物线上一动点,且位于第一象限,直线与y轴交于点G.
(1)、求点B的坐标及直线的解析式:(2)、当二次函数的自变量x满足时,此函数的最大值为p,最小值为q,且.求m的值:(3)、平移抛物线 , 使其顶点始终在直线上移动,当平移后的抛物线与射线BA只有一个公共点时,设此时抛物线的顶点的横坐标为n,请直接写出n的取值范围.21. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,点B的坐标是 , 顶点C的坐标是 , M是抛物线上一动点,且位于第一象限,直线与y轴交于点G. (1)、求该抛物线的解析式;(2)、如图1,N是抛物线上一点,且位于第二象限,连接 , 记的面积分别为 . 当 , 且直线时,求证:点N与点M关于y轴对称;(3)、如图2,直线与y轴交于点H,是否存在点M,使得 . 若存在,求出点M的坐标;若不存在,请说明理由.22. 在平面直角坐标系中,直线y=﹣x﹣2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a>0)经过A,B两点,并与x轴的正半轴交于点C.
(1)、求该抛物线的解析式;(2)、如图1,N是抛物线上一点,且位于第二象限,连接 , 记的面积分别为 . 当 , 且直线时,求证:点N与点M关于y轴对称;(3)、如图2,直线与y轴交于点H,是否存在点M,使得 . 若存在,求出点M的坐标;若不存在,请说明理由.22. 在平面直角坐标系中,直线y=﹣x﹣2与x轴交于点A,与y轴交于点B,抛物线y=ax2+bx+c(a>0)经过A,B两点,并与x轴的正半轴交于点C.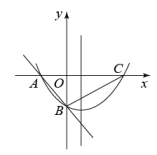
 (1)、求a,b满足的关系式及c的值;(2)、当a=时,若点P是抛物线对称轴上的一个动点,求△PAB周长的最小值;(3)、当a=1时,若点Q是直线AB下方抛物线上的一个动点,过点Q作QD⊥AB于点D,当QD的值最大时,求此时点Q的坐标及QD的最大值.23. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,顶点为 , 抛物线的对称轴交直线于点E.
(1)、求a,b满足的关系式及c的值;(2)、当a=时,若点P是抛物线对称轴上的一个动点,求△PAB周长的最小值;(3)、当a=1时,若点Q是直线AB下方抛物线上的一个动点,过点Q作QD⊥AB于点D,当QD的值最大时,求此时点Q的坐标及QD的最大值.23. 如图,在平面直角坐标系中,抛物线与x轴交于A,B两点,与y轴交于点C,顶点为 , 抛物线的对称轴交直线于点E. (1)、求抛物线的表达式;(2)、把上述抛物线沿它的对称轴向下平移,平移的距离为 , 在平移过程中,该抛物线与直线始终有交点,求h的最大值;(3)、M是(1)中抛物线上一点,N是直线上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.24. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.
(1)、求抛物线的表达式;(2)、把上述抛物线沿它的对称轴向下平移,平移的距离为 , 在平移过程中,该抛物线与直线始终有交点,求h的最大值;(3)、M是(1)中抛物线上一点,N是直线上一点.是否存在以点D,E,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.24. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.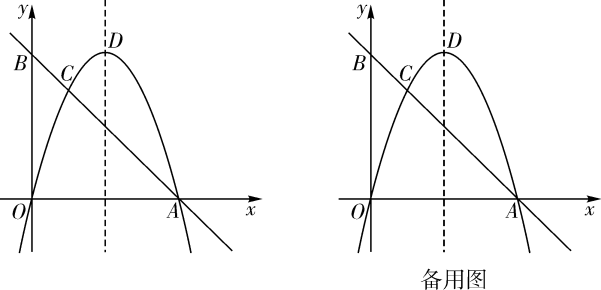 (1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.