2022年秋季浙教版数学九年级上册第一章《二次函数》单元测试A
试卷更新日期:2022-09-15 类型:单元试卷
一、单选题(每题3分,共30分)
-
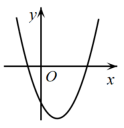
1. 将抛物线y=x2向上平移3个单位,所得抛物线的解析式是( )A、y=x2+3 B、y=x2-3 C、y=(x+3)2 D、y=(x-3)22. 已知二次函数 , 当时,y的最小值为 , 则a的值为( )A、或4 B、或 C、或4 D、或43. 已知二次函数 ,当函数值y随x值的增大而增大时,x的取值范围是( )A、 B、 C、 D、4. 根据如图所示的二次函数的图象,判断反比例函数与一次函数的图象大致是( )
 A、
A、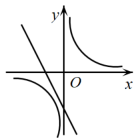 B、
B、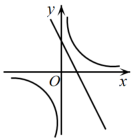 C、
C、 D、
D、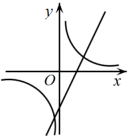 5. 抛物线y=x2+x+c与x轴只有一个公共点,则c的值为( )A、 B、 C、 D、46. 在平面直角坐标系中,将二次函数的图象向左平移1个单位长度,再向下平移2个单位长度,所得函数的解析式为( )A、 B、 C、 D、7. 已知抛物线y=ax2 +bx +c的对称轴为x=1,与x轴正半轴的交点为A(3,0),其部分图象如图所示,有下列结论:①abc >0;②2c﹣3b <0;③5a +b+2c=0;④若B( , y1)、C( , y2)、D( , y3)是抛物线上的三点,则y1<y2<y3.其中正确结论的个数有( )
5. 抛物线y=x2+x+c与x轴只有一个公共点,则c的值为( )A、 B、 C、 D、46. 在平面直角坐标系中,将二次函数的图象向左平移1个单位长度,再向下平移2个单位长度,所得函数的解析式为( )A、 B、 C、 D、7. 已知抛物线y=ax2 +bx +c的对称轴为x=1,与x轴正半轴的交点为A(3,0),其部分图象如图所示,有下列结论:①abc >0;②2c﹣3b <0;③5a +b+2c=0;④若B( , y1)、C( , y2)、D( , y3)是抛物线上的三点,则y1<y2<y3.其中正确结论的个数有( )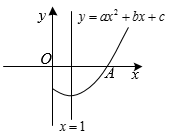 A、1 B、2 C、3 D、48. 二次函数的图象如图所示,则一次函数的图象经过( )
A、1 B、2 C、3 D、48. 二次函数的图象如图所示,则一次函数的图象经过( )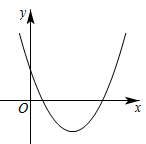 A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限9. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .
A、第一、二、三象限 B、第一、二、四象限 C、第一、三、四象限 D、第二、三、四象限9. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .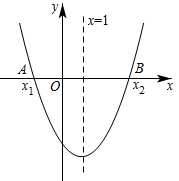
正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个10. 抛物线与y轴交于点C,过点C作直线l垂直于y轴,将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G,点 , 为图形G上两点,若 , 则m的取值范围是( )A、或 B、 C、 D、二、填空题(每题3分,共18分)
-
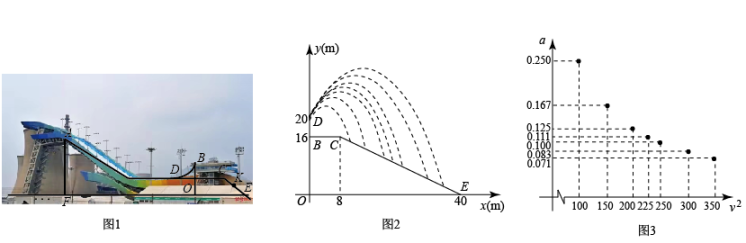
11. 根据物理学规律,如果不考虑空气阻力,以的速度将小球沿与地面成角的方向击出,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间的函数关系是 , 当飞行时间t为s时,小球达到最高点.12. 如图,是一名男生推铅球时,铅球行进过程中形成的抛物线.按照图中所示的平面直角坐标系,铅球行进高度y(单位:m)与水平距离x(单位:m)之间的关系是 , 则铅球推出的水平距离OA的长是m.
 13. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).
13. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).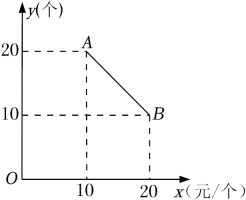 14. 在平面直角坐标系中,点和点的坐标分别为和 , 抛物线与线段只有一个公共点,则的取值范围是 .15. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个.
14. 在平面直角坐标系中,点和点的坐标分别为和 , 抛物线与线段只有一个公共点,则的取值范围是 .15. 已知二次函数 , 图象的一部分如图所示,该函数图象经过点 , 对称轴为直线.对于下列结论:①;②;③;④(其中);⑤若和均在该函数图象上,且 , 则.其中正确结论的个数共有个. 16. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:
16. 已知抛物线( , , 是常数)开口向下,过 , 两点,且.下列四个结论:①;
②若 , 则;
③若点 , 在抛物线上, , 且 , 则;
④当时,关于的一元二次方程必有两个不相等的实数根.
其中正确的是(填写序号).
三、解答题(共8题,共72分)
-
17. 某超市采购了两批同样的冰墩墩挂件,第一批花了6600元,第二批花了8000元,第一批每个挂件的进价是第二批的1.1倍,且第二批比第一批多购进50个.(1)、求第二批每个挂件的进价;(2)、两批挂件售完后,该超市以第二批每个挂件的进价又采购一批同样的挂件,经市场调查发现,当售价为每个60元时,每周能卖出40个,若每降价1元,每周多卖10个,由于货源紧缺,每周最多能卖90个,求每个挂件售价定为多少元时,每周可获得最大利润,最大利润是多少?18. 根据以下素材,探索完成任务.
如何设计拱桥景观灯的悬挂方案?
素材1
图1中有一座拱桥,图2是其抛物线形桥拱的示意图,某时测得水面宽 20m ,拱顶离水面 5m .据调查,该河段水位在此基础上再涨 1.8m 达到最高.
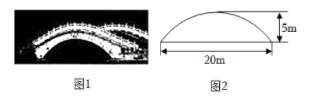
素材2
为迎佳节,拟在图1桥洞前面的桥拱上悬挂 40cm 长的灯笼,如图3.为了安全,灯笼底部距离水面不小于 1m ;为了实效,相邻两盏灯笼悬挂点的水平间距均为 1.6m ;为了美观,要求在符合条件处都挂上灯笼,且挂满后成轴对称分布.
问题解决
任务1
确定桥拱形状
在图2中建立合适的直角坐标系,求抛物线的函数表达式.
任务2
探究悬挂范围
在你所建立的坐标系中,仅在安全的条件下,确定悬挂点的纵坐标的最小值和横坐标的取值范围.
任务3
拟定设计方案
给出一种符合所有悬挂条件的灯笼数量,并根据你所建立的坐标系,求出最左边一盏灯笼悬挂点的横坐标.
19. 已知二次函数的自变量的部分取值和对应函数值如下表:…
0
1
2
3
…
…
4
3
0
…
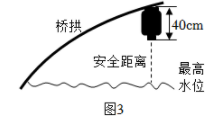
(1)、求二次函数的表达式;(2)、将二次函数的图象向右平移个单位,得到二次函数的图象,使得当时,随增大而增大;当时,随增大而减小,请写出一个符合条件的二次函数的表达式 , 实数的取值范围是;(3)、、、是二次函数的图象上互不重合的三点.已知点、的横坐标分别是、 , 点与点关于该函数图象的对称轴对称,求的度数.20. 如图1为北京冬奥会“雪飞天”滑雪大跳台赛道的横截面示意图.取水平线OE为x轴,铅垂线OD为y轴,建立平面直角坐标系.运动员以速度从D点滑出,运动轨迹近似抛物线 . 某运动员7次试跳的轨迹如图2.在着陆坡CE上设置点K(与DO相距32m)作为标准点,着陆点在K点或超过K点视为成绩达标.(参考数据: , )
 (1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.
(1)、求线段CE的函数表达式(写出的取值范围).(2)、当时,着陆点为P,求P的横坐标并判断成绩是否达标.(3)、在试跳中发现运动轨迹与滑出速度v的大小有关,进一步探究,测算得7组a与 的对应数据,在平面直角坐标系中描点如图3.①猜想a关于的函数类型,求函数表达式,并任选一对对应值验证.
②当v为多少m/s时,运动员的成绩恰能达标(精确到1m/s)?
21. 在平面直角坐标系xOy中,已知抛物线y=-x2+2mx+3m,点A(3,0).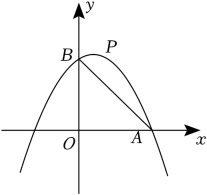 (1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.22. 如图,平面直角坐标系中,O是坐标原点,抛物线经过点和点与x轴另一个交点A.抛物线与y轴交于点C,作直线AD.
(1)、当抛物线过点A时,求抛物线的解析式;(2)、证明:无论m为何值,抛物线必过定点D,并求出点D的坐标;(3)、在(1)的条件下,抛物线与y轴交于点B,点P是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与y轴交于点N.设S=S△PAM-S△BMN,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值;若不存在,请说明理由.22. 如图,平面直角坐标系中,O是坐标原点,抛物线经过点和点与x轴另一个交点A.抛物线与y轴交于点C,作直线AD. (1)、①求抛物线的函数表达式
(1)、①求抛物线的函数表达式②并直接写出直线AD的函数表达式.
(2)、点E是直线AD下方抛物线上一点,连接BE交AD于点F,连接BD,DE,的面积记为 , 的面积记为 , 当时,求点E的坐标;(3)、点G为抛物线的顶点,将抛物线图象中x轴下方部分沿x轴向上翻折,与抛物线剩下部分组成新的曲线为 , 点C的对应点 , 点G的对应点 , 将曲线 , 沿y轴向下平移n个单位长度().曲线与直线BC的公共点中,选两个公共点作点P和点Q,若四边形是平行四边形,直接写出P的坐标.23. 如图,在平面直角坐标系中,抛物线y=ax2+bx+2经过A( , 0),B(3,)两点,与y轴交于点C.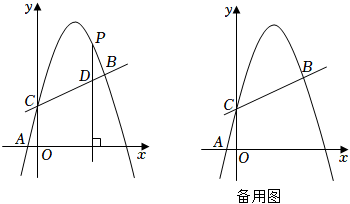 (1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.24. 如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.
(1)、求抛物线的解析式;(2)、点P在抛物线上,过P作PD⊥x轴,交直线BC于点D,若以P、D、O、C为顶点的四边形是平行四边形,求点P的横坐标;(3)、抛物线上是否存在点Q,使∠QCB=45°?若存在,请直接写出点Q的坐标;若不存在,请说明理由.24. 如图,已知直线y=x+4与x轴交于点A,与y轴交于点C,抛物线y=ax2+bx+c经过A,C两点,且与x轴的另一个交点为B,对称轴为直线x=﹣1.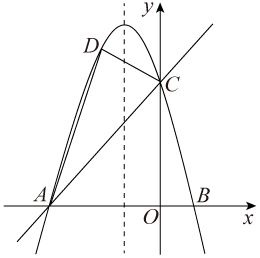 (1)、求抛物线的表达式;(2)、D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、D是第二象限内抛物线上的动点,设点D的横坐标为m,求四边形ABCD面积S的最大值及此时D点的坐标;(3)、若点P在抛物线对称轴上,是否存在点P,Q,使以点A,C,P,Q为顶点的四边形是以AC为对角线的菱形?若存在,请求出P,Q两点的坐标;若不存在,请说明理由.