2022年秋季北师版数学九年级上册第一章《特殊的平行四边形》检测练习B卷
试卷更新日期:2022-09-14 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 下列命题,其中是真命题的是( )A、对角线互相垂直的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、对角线互相平分的四边形是菱形 D、对角线互相垂直的矩形是正方形2. 如图,在菱形ABCD中, , M是对角线BD上的一个动点, , 则的最小值为( )
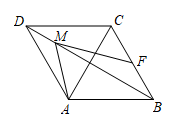 A、1 B、 C、 D、23. 正方形的对角线相交于点O(如图1),如果绕点O按顺时针方向旋转,其两边分别与边相交于点E、F(如图2),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是( )
A、1 B、 C、 D、23. 正方形的对角线相交于点O(如图1),如果绕点O按顺时针方向旋转,其两边分别与边相交于点E、F(如图2),连接EF,那么在点E由B到A的过程中,线段EF的中点G经过的路线是( ) A、线段 B、圆弧 C、折线 D、波浪线4. 如图,在四边形纸片中, , , . 将纸片折叠,使点落在边上的点处,折痕为 . 若 , 则的长为( )
A、线段 B、圆弧 C、折线 D、波浪线4. 如图,在四边形纸片中, , , . 将纸片折叠,使点落在边上的点处,折痕为 . 若 , 则的长为( )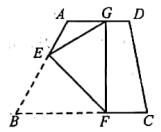 A、5 B、 C、 D、5. 如图,在平行四边形ABCD中,对角线 , , , 为 的中点,E为边 上一点,直线 交 于点F,连结 , .下列结论不成立的是( )
A、5 B、 C、 D、5. 如图,在平行四边形ABCD中,对角线 , , , 为 的中点,E为边 上一点,直线 交 于点F,连结 , .下列结论不成立的是( ) A、四边形 为平行四边形 B、若 ,则四边形 为矩形 C、若 ,则四边形 为菱形 D、若 ,则四边形 为正方形6. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点 处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( )
A、四边形 为平行四边形 B、若 ,则四边形 为矩形 C、若 ,则四边形 为菱形 D、若 ,则四边形 为正方形6. 如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF;把纸片展平后再次折叠,使点A落在EF上的点 处,得到折痕BM,BM与FF相交于点N.若直线B A’交直线CD于点O,BC=5,EN=1,则OD的长为( ) A、 B、 C、 D、7. 如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为( )
A、 B、 C、 D、7. 如图,将矩形 折叠,使点C和点A重合,折痕为 , 与 交于点O若 , ,则 的长为( )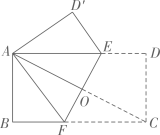 A、 B、 C、 D、8. 如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )A、互相平分 B、相等 C、互相垂直 D、互相垂直平分9. 如图,矩形 中, 相交于点O , 过点B作 交 于点F , 交 于点M , 过点D作 交 于点E , 交 于点N , 连接 .则下列结论:
A、 B、 C、 D、8. 如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是( )A、互相平分 B、相等 C、互相垂直 D、互相垂直平分9. 如图,矩形 中, 相交于点O , 过点B作 交 于点F , 交 于点M , 过点D作 交 于点E , 交 于点N , 连接 .则下列结论:① ;② ;③ ;④当 时,四边形 是菱形.其中,正确结论的个数是( )
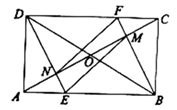 A、1个 B、2个 C、3个 D、4个10. 如图,正方形 ,点 在边 上,且 , ,垂足为 ,且交 于点 , 与 交于点 ,延长 至 ,使 ,连接 .有如下结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是( )
A、1个 B、2个 C、3个 D、4个10. 如图,正方形 ,点 在边 上,且 , ,垂足为 ,且交 于点 , 与 交于点 ,延长 至 ,使 ,连接 .有如下结论:① ;② ;③ ;④ .上述结论中,所有正确结论的序号是( )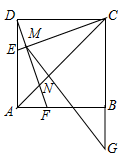 A、①② B、①③ C、①②③ D、②③④
A、①② B、①③ C、①②③ D、②③④二、填空题(每题3分,共18分)
-
11. 如图,矩形纸片ABCD,AB=6cm,BC=8cm,E为边CD上一点.将△BCE沿BE所在的直线折叠,点C恰好落在AD边上的点F处,过点F作FM⊥BE,垂足为点M,取AF的中点N,连接MN,则MN=cm.
 12. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .
12. 如图, , 是正方形 的对角线 上的两点, , ,则四边形 的周长是 .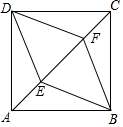 13. 如图,已知菱形ABCD的周长为16,面积为8 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 .
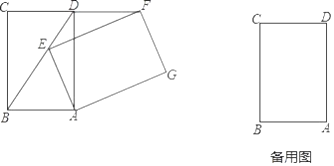
13. 如图,已知菱形ABCD的周长为16,面积为8 ,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为 . 14. 如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD边上,记为B′,折痕为CE,再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE= BC.则矩形纸片ABCD的面积为 .
14. 如图,将一张矩形纸片ABCD的边BC斜着向AD边对折,使点B落在AD边上,记为B′,折痕为CE,再将CD边斜向下对折,使点D落在B′C边上,记为D′,折痕为CG,B′D′=2,BE= BC.则矩形纸片ABCD的面积为 .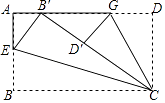 15. 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AE=4,则△EBF周长的大小为 .
15. 如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上的E处,EQ与BC相交于点F,若AD=8,AE=4,则△EBF周长的大小为 .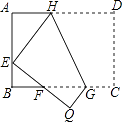 16. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5 cm,且tan∠EFC= ,那么矩形ABCD的周长为cm.
16. 如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5 cm,且tan∠EFC= ,那么矩形ABCD的周长为cm.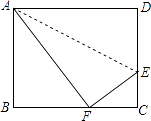
三、解答题(共8题,共72分)
-
17. 如图,在菱形 中,点 、 分别在 、 上,且 ,求证: .
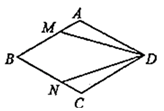 18. 如图,在 中,对角线 与 相交于点O,点E,F分别在 和 的延长线上,且 ,连接 , .
18. 如图,在 中,对角线 与 相交于点O,点E,F分别在 和 的延长线上,且 ,连接 , . (1)、求证: ≌ ;(2)、连接 , ,当 平分 时,四边形 是什么特殊四边形?请说明理由.19. 如图,过▱ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB、BC.CD、DA于点P、M、Q、N.
(1)、求证: ≌ ;(2)、连接 , ,当 平分 时,四边形 是什么特殊四边形?请说明理由.19. 如图,过▱ABCD对角线AC与BD的交点E作两条互相垂直的直线,分别交边AB、BC.CD、DA于点P、M、Q、N. (1)、求证: PBE≌ QDE;(2)、顺次连接点P、M、Q、N,求证:四边形PMQN是菱形.20. 如图,在中,交于点 , 点在上, .
(1)、求证: PBE≌ QDE;(2)、顺次连接点P、M、Q、N,求证:四边形PMQN是菱形.20. 如图,在中,交于点 , 点在上, .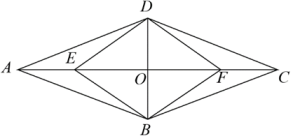 (1)、求证:四边形是平行四边形;(2)、若求证:四边形是菱形.21. 如图,矩形 中,点 在边 上,将 沿 折叠,点 落在 边上的点 处,过点 作 交 于点 ,连接 .
(1)、求证:四边形是平行四边形;(2)、若求证:四边形是菱形.21. 如图,矩形 中,点 在边 上,将 沿 折叠,点 落在 边上的点 处,过点 作 交 于点 ,连接 .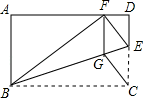 (1)、求证:四边形 是菱形;(2)、若 ,求四边形 的面积.22. 四边形ABCD为矩形,E是AB延长线上的一点.
(1)、求证:四边形 是菱形;(2)、若 ,求四边形 的面积.22. 四边形ABCD为矩形,E是AB延长线上的一点.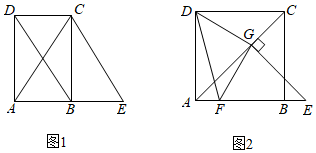 (1)、若AC=EC , 如图1,求证:四边形BECD为平行四边形;(2)、若AB=AD , 点F是AB上的点,AF=BE , EG⊥AC于点G , 如图2,求证:△DGF是等腰直角三角形.
(1)、若AC=EC , 如图1,求证:四边形BECD为平行四边形;(2)、若AB=AD , 点F是AB上的点,AF=BE , EG⊥AC于点G , 如图2,求证:△DGF是等腰直角三角形.