2022年苏科版初中数学七年级上册3.6 整式的加减同步练习

试卷更新日期：2022-09-14 类型：同步测试

进入出卷网下载

一、夯实基础

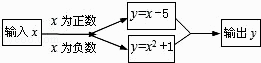
1. 计算 $- 3 (x - 2 y) + 4 (x - 2 y)$ 的结果是（）

A、x-2y B、x+2 C、-x-2y D、-x+2y

查看试题解析
2. 计算b²-2ab+a²与-3b²+ab的差为（）

A、4b²-3ab+a² B、- 4b²+3ab-a² C、4b²+3ab-a² D、a²-4b²-ab

查看试题解析
3. 已知长方形的一边长为3a﹣2b，另一边比它长a﹣b，则此长方形的另一边长为（）

A、4a﹣b B、4a﹣3b C、2a﹣3b D、2a﹣b

查看试题解析
4. 下面是小明做的一道多项式的加减运算题，但他不小心把一滴墨水滴在了上面. $(- x^{2} + 3 x y - \frac{1}{2} y^{2}) - (- \frac{1}{2} x^{2} + 4 x y - \frac{1}{2} y^{2}) = - \frac{1}{2} x^{2} ●$ ，黑圆处即为被墨汁遮住的部分，那么被墨汁遮住的部分是（）

A、 $- x y - y_{2}$ B、 $- x y$ C、 $- 7 x y$ D、 $+ 7 x y$

查看试题解析
5. 设A＝3x²﹣3x+5，B＝2x²﹣3x﹣2，若x取任意实数，则A与B的大小关系为（　　）

A、A＞B B、A＜B C、A＝B D、无法比较

查看试题解析
6. 计算： $4 x + 3 y - 2 (2 x - y) =$ ．

查看试题解析
7. 一个多项式加上2x²﹣4x﹣3得-x²﹣3x，则这个多项式为．

查看试题解析
8. 减去 $- 3 m$ 等于 $m^{2} + 3 m + 2$ 的多项式是.

查看试题解析
9. 若 $a - b = 2 ， b - c = - 3$ ，则 $a - c$ 等于．

查看试题解析
10. 根据如图所示的计算程序，若输入的值x=﹣1，则输出的值y= ．

查看试题解析
11. 计算

(1)、 $- a^{2} b + (3 a b^{2} - a^{2} b) - 2 (2 a b^{2} - a^{2} b)$

(2)、 $3 x^{2} y - (x y - 3 x y^{2}) - [2 x y^{2} - 2 (x y - \frac{3}{2} x^{2} y)]$

查看试题解析
12. 一个多项式减去 $\frac{2}{3}$ x²﹣ $\frac{2}{3}$ xy﹣ $\frac{2}{3}$ 的差是﹣ $\frac{1}{2}$ x²＋2xy﹣ $\frac{1}{4}$ ，求这个多项式．

查看试题解析
13. 已知多项式 $A = 2 x^{2} - 3 x y + 2 y^{2}$ ， $B = 2 x^{2} + x y - 3 y^{2}$ ，如果 $A + B + C = 0$ ，求多项式C．

查看试题解析
14. 已知A＝5x²﹣mx+n，B＝3x²﹣2x+1．

(1)、若m为最小的正整数，且m+n＝0，求A﹣B；

(2)、若A﹣B的结果中不含关于x的一次项和常数项，求m²+n²﹣2mn的值．

查看试题解析

二、能力提优

15. 今天数学课上，老师讲了多项式的加减，小明做作业时突然发现一道题﹣x²+3xy﹣y²+ $\frac{1}{2}$ x²-4xy+2y²=﹣ $\frac{1}{2}$ x²+________+y²空格的地方被钢笔水弄污了，那么空格中的一项是（）

A、7xy B、﹣7xy C、xy D、﹣xy

查看试题解析
16. 若 $M$ 和 $N$ 都是三次多项式，则 $M + N$ 一定是（）

A、次数低于三次的整式 B、六次多项式 C、三次多项式 D、次数不高于三次的整式

查看试题解析
17. 某商店在甲批发市场以每包a元的价格进了50包茶叶，又在乙批发市场以每包b元（a＞b）的价格进了同样的70包茶叶，如果以每包 $\frac{a + b}{2}$ 元价格全部卖出这种茶叶，那么这家商店（）

A、盈利了 B、亏损了 C、不盈不亏 D、盈亏不能确定

查看试题解析
18. 为求1+2+2²+2³+…+2²⁰¹⁵的值，可令S=1+2+2²+2³+…+2²⁰¹⁵ ，则2S=2+2²+2³+…+2²⁰¹⁶ ，因此2S﹣S=2²⁰¹⁶﹣1.仿照以上推理，计算出1+5+5²+5³+…+5²⁰¹⁵的值为（）

A、5²⁰¹⁵﹣1 B、5²⁰¹⁶﹣1 C、 $\frac{5^{2015} - 1}{4}$ D、 $\frac{5^{2016} - 1}{4}$

查看试题解析
19. 把如图1的两张大小相同的长方形卡片放置在图2与图3中的两个相同大长方形中，已知这两个大长方形的长比宽长20cm，若记图2中阴影部分的周长为C₁ ，图3中阴影部分的周长为C₂ ，那么C₁-C₂=（）

A、10cm B、20cm C、30cm D、40cm

查看试题解析
20. 化简： $2 x^{2} + 1 - 3 x + 7 - 2 x^{2} + 5 x =$ .

查看试题解析
21. 已知三角形第一边的长为 $2 a + b$ ，第二边比第一边长a-b，第三边比第二边短a，则这个三角形的周长是（用含字母的代数式表示）

查看试题解析
22. 有理数 $a$ ， $b$ ， $c$ 在数轴上的对应点如图所示，化简： $| a + b | - | b - c | + | c - a - b | =$ ．

查看试题解析
23. 化简：

(1)、 $(2 x^{2} - \frac{1}{2} + 3 x) - 4 (x - x^{2} + \frac{1}{2})$ ；

(2)、 $3 x^{2} - [7 x - (- 3 + 4 x) - 2 x^{2}]$ .

查看试题解析
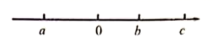24. 在计算代数式 $(2 x^{3} - 3 x^{2} y - 2 x y^{2}) - (x^{3} - 2 x y^{2} + y^{3}) + (- x^{3} + 3 x^{2} y - y^{3})$ 的值，其中 $x = 0.5$ ， $y = - 1$ 时，甲同学把 $x = 0.5$ 错抄成 $x = - 0.5$ ，但他计算的结果是正确的.试说明理由，并求出这个结果.

查看试题解析
25. 马虎的李明在计算多项式M加上 $x^{2} - 3 x + 7$ 时，因错看成加上 $x^{2} + 3 x + 7$ ，尽管计算过程没有错误，也只能得到一个错误的答案为 $5 x^{2} + 2 x - 4$ .

(1)、求多项式M；

(2)、求出本题的正确答案.

查看试题解析
26. 已知： $A = 3 m x - x$ ， $B = - m x - 3 x + m$ .

(1)、化简： $3 A - 2 B$ ；

(2)、若 $3 A - 2 B$ 的值与字母m的取值无关，求x的值.

查看试题解析
27. 已知a，b，c在数轴上的位置如图所示，
求|a+b|﹣3|b+c|+2|a﹣b|﹣|c﹣b|的值.

查看试题解析
28. 印卷时，工人不小心把一道化简题前面一个数字遮住了，结果变成：■ $x^{2} y - [5 x y^{2} - 2 (- \frac{2}{3} x y + \frac{3}{2} x^{2} y) - \frac{4}{3} x y] + 5 x y^{2}$ ．

(1)、某同学辨认后把“■”猜成10，请你帮他算算化简后该式是多少；

(2)、老师说：“你猜错了，我看到该题目遮挡部分是单项式 $- \frac{4 m^{2} n}{3}$ 的系数和次数之积．”遮挡部分是多少？

(3)、若化简结果是一个常数，请算算遮挡部分又该是多少？

查看试题解析

三、延伸拓展

29. 如图，将图1中的长方形纸片前成（1）号、（2）号、（3）号、（4）号正方形和（5）号长方形，并将它们按图2的方式无重叠地放入另一个大长方形中，若需求出没有覆盖的阴影部分的周长，则下列说法中错误的是（）

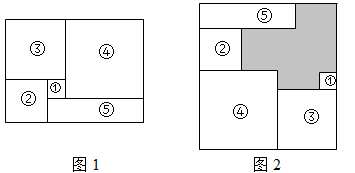A、只需知道图 1 中大长方形的周长即可 B、只需知道图 2 中大长方形的周长即可 C、只需知道（3）号正方形的周长即可 D、只需知道（5）号长方形的周长即可

查看试题解析
30. 如图，长为y（cm），宽为x（cm）的大长方形被分割为7小块，除阴影A，B外，其余5块是形状、大小完全相同的小长方形，其较短的边长为4cm，下列说法中正确的有（）
①小长方形的较长边为y﹣12；

②阴影A的较短边和阴影B的较短边之和为x﹣y+4；

③若x为定值，则阴影A和阴影B的周长和为定值；

④当x＝20时，阴影A和阴影B的面积和为定值.

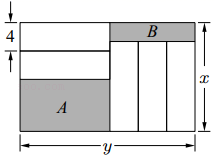A、1个 B、2个 C、3个 D、4个

查看试题解析
31. 七年级学习代数式求值时，遇到这样一类题“代数式 $a x - y + 6 + 3 x - 5 y - 1$ 的值与 $x$ 的取值无关，求 $a$ 的值”，通常的解题方法是：把x、y看作字母，a看作系数合并同类项，因为代数式的值与x的取值无关，所以含 $x$ 项的系数为0，
即原式＝ $(a + 3) x - 6 y + 5$ ，所以 $a + 3 = 0$ ，则 $a = - 3$ ．

(1)、若关于 $x$ 的多项式 $(2 x - 3) m + 2 m^{2} - 3 x$ 的值与 $x$ 的取值无关，求 $m$ 值；

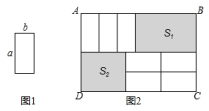(2)、已知A $= 2 x^{2} + 3 x y - 2 x - 1$ ， B $= - x^{2} + x y - 1$ ；且3A＋6B的值与 $x$ 无关，求 $y$ 的值；

(3)、7张如图1的小长方形，长为a，宽为b，按照图2方式不重叠地放在大长方形ABCD内，大长方形中未被覆盖的两个部分（图中阴影部分），设右上角的面积为 $S_{1}$ ，左下角的面积为 $S_{2}$ ，当AB的长变化时， $S_{1} - S_{2}$ 的值始终保持不变，求 $a$ 与 $b$ 的等量关系．

查看试题解析

2022年苏科版初中数学七年级上册3.6 整式的加减 同步练习

一、夯实基础

二、能力提优

三、延伸拓展

2022年苏科版初中数学七年级上册3.6 整式的加减同步练习