浙江省诸暨市浣江教育共同体2021-2022学年九年级上学期期中考试数学试题
试卷更新日期:2022-09-14 类型:期中考试
一、单选题
-
1. 抛物线y=2(x+3)2+4的顶点是( )A、(3,4) B、(3,-4) C、(-3,4) D、(4,-3)2. 学校招募运动会广播员,从三名男生和一名女生共四名候选人中随机选取一人,则选中男生的概率为( )A、 B、 C、 D、3.
已知:如图,OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB的度数为( )
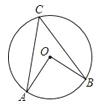 A、45° B、35° C、25° D、20°4.
A、45° B、35° C、25° D、20°4.下列四个三角形中,与图中的三角形相似的是( )
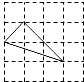 A、
A、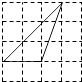 B、
B、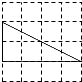 C、
C、 D、
D、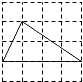 5. 把抛物线向上平移1个单位,再向右平移3个单位,得到的抛物线是( )A、 B、 C、 D、+26. 如图,电路图上有 个开关 、 、 、 和 个小灯泡,同时闭合开关 、 或同时闭合开关 、 都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )
5. 把抛物线向上平移1个单位,再向右平移3个单位,得到的抛物线是( )A、 B、 C、 D、+26. 如图,电路图上有 个开关 、 、 、 和 个小灯泡,同时闭合开关 、 或同时闭合开关 、 都可以使小灯泡发光.下列操作中,“小灯泡发光”这个事件是随机事件的是( )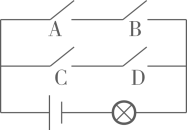 A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关7. 如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )
A、只闭合1个开关 B、只闭合2个开关 C、只闭合3个开关 D、闭合4个开关7. 如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )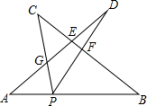 A、△CGE∽△CBP B、△APD∽△PGD C、△APG∽△BFP D、△PCF∽△BCP8. 在直角坐标平面内,点A的坐标为(3,0),点B的坐标为(a,0),圆A的半径为4,下列说法中不正确的是( )A、当a=﹣1时,点B在圆A上 B、当a<7时,点B在圆A内 C、当a<﹣1时,点B在圆A外 D、当﹣1<a<7时,点B在圆A内9. 如图所示,△ABC中,AD⊥BC于D,对于下列中的每一个条件:①∠B+∠DAC=90°;②∠B=∠DAC;③CD:AD=AC:AB;④AB2=BD·BC,其中一定能判定△ABC是直角三角形的共有( )
A、△CGE∽△CBP B、△APD∽△PGD C、△APG∽△BFP D、△PCF∽△BCP8. 在直角坐标平面内,点A的坐标为(3,0),点B的坐标为(a,0),圆A的半径为4,下列说法中不正确的是( )A、当a=﹣1时,点B在圆A上 B、当a<7时,点B在圆A内 C、当a<﹣1时,点B在圆A外 D、当﹣1<a<7时,点B在圆A内9. 如图所示,△ABC中,AD⊥BC于D,对于下列中的每一个条件:①∠B+∠DAC=90°;②∠B=∠DAC;③CD:AD=AC:AB;④AB2=BD·BC,其中一定能判定△ABC是直角三角形的共有( )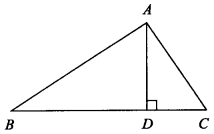 A、3个 B、2个 C、1个 D、0个10. 定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点A(0,2),点C(2,0),则互异二次函数y=(x﹣m)2﹣m与正方形OABC有交点时m的最大值和最小值之差为( )
A、3个 B、2个 C、1个 D、0个10. 定义:我们将顶点的横坐标和纵坐标互为相反数的二次函数称为“互异二次函数”.如图,在正方形OABC中,点A(0,2),点C(2,0),则互异二次函数y=(x﹣m)2﹣m与正方形OABC有交点时m的最大值和最小值之差为( )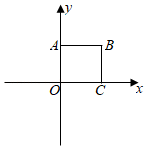 A、5 B、 C、4 D、
A、5 B、 C、4 D、二、填空题
-
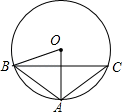
11. 已知 ,则 =.12. 一个均匀材料制作的正方形骰子,各个面上分别标有数字1,2,3,4,5,6,连续抛掷两次,点数之和为6的概率是 .13. 如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC= .
 14. 已知二次函数 的部分图象如图所示,则一元二次方程 的解为:.
14. 已知二次函数 的部分图象如图所示,则一元二次方程 的解为:.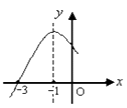 15. 如图,在5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与BD交于E,则图中阴影部分的面积为.(结果保留 )
15. 如图,在5×3的网格图中,每个小正方形的边长均为1,设经过图中格点A,C,B三点的圆弧与BD交于E,则图中阴影部分的面积为.(结果保留 ) 16. 如图,在Rt△ABC中,∠B=90°,BC =2 AB = 8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,当△EDC旋转到A,D,E三点共线时,线段BD的长为 .
16. 如图,在Rt△ABC中,∠B=90°,BC =2 AB = 8,点D,E分别是边BC,AC的中点,连接DE.将△EDC绕点C按顺时针方向旋转,当△EDC旋转到A,D,E三点共线时,线段BD的长为 .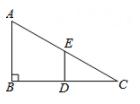
三、解答题
-
17. 一只不透明的袋子中装有1个白球、2个黄球和1个红球,每个球除颜色外都相同,将球摇匀.(1)、求从中任意摸出1个白球的概率.(2)、从中任意摸出2个球,请利用画树状图或列表法,求出摸到2个都是黄球的概率.18. 如图,一圆弧过方格的格点A、B、C,在方格中建立平面直角坐标系,使点A的坐标为 ,
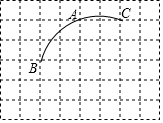
(1)画出平面直角坐标系.
(2)仅用一把无刻度的直尺,利用网格,找出该圆弧的圆心并直接写出圆心的坐标.(不写作法,保留作图痕迹)19. 如图,在矩形中,E是的中点, , 垂足为F.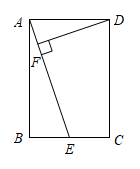 (1)、求证:;(2)、若AB=12,BC=10,求的长.20. 已知在中, , 以AB为直径的⊙O分别交AC于D,BC于E,连接ED.
(1)、求证:;(2)、若AB=12,BC=10,求的长.20. 已知在中, , 以AB为直径的⊙O分别交AC于D,BC于E,连接ED.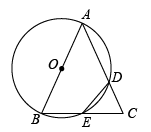 (1)、求证:;(2)、若CD= , , 求AB的长.21. 如图,二次函数图象与x轴交于点A、B,与y轴交与点C,抛物线的顶点坐标是(2,9),且经过D(3,8).
(1)、求证:;(2)、若CD= , , 求AB的长.21. 如图,二次函数图象与x轴交于点A、B,与y轴交与点C,抛物线的顶点坐标是(2,9),且经过D(3,8).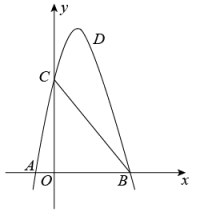 (1)、求抛物线的函数关系式;(2)、求△ABC的面积;(3)、在抛物线的对称轴上是否存在一点M,使得BM+DM最短?若存在,求出M的坐标.若不存在,请说明理由.22. 红星公司销售一种成本为50元/件的产品,原月销售单价为60元/件.一个月可售出5万件,现公司打算提价销售,经市场调查表明,当月销售单价每涨价1元,月销售量就减少0.1万件.设月销售单价为x元/件,月销售量为y万件,月销售利润为w万元.(1)、求出y与x之间的函数关系式,不需要写出自变量x的取值范围;(2)、当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元?(3)、为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向贫困山区捐款a元.已知该公司捐款当月的月销售单价不高于80元/件,月销售最大利润是78万元,求a的值.23. 【了解概念】
(1)、求抛物线的函数关系式;(2)、求△ABC的面积;(3)、在抛物线的对称轴上是否存在一点M,使得BM+DM最短?若存在,求出M的坐标.若不存在,请说明理由.22. 红星公司销售一种成本为50元/件的产品,原月销售单价为60元/件.一个月可售出5万件,现公司打算提价销售,经市场调查表明,当月销售单价每涨价1元,月销售量就减少0.1万件.设月销售单价为x元/件,月销售量为y万件,月销售利润为w万元.(1)、求出y与x之间的函数关系式,不需要写出自变量x的取值范围;(2)、当月销售单价是多少元/件时,月销售利润最大,最大利润是多少万元?(3)、为响应国家“乡村振兴”政策,该公司决定在某月每销售1件产品便向贫困山区捐款a元.已知该公司捐款当月的月销售单价不高于80元/件,月销售最大利润是78万元,求a的值.23. 【了解概念】在凸四边形中,若一边与它的两条邻边组成的两个内角相等,则称该四边形为邻等四边形,这条边叫做这个四边形的邻等边.
(1)、【理解运用】
邻等四边形ABCD中,∠A=30°,∠B=70°,则∠C的度数为 .(2)、如图,凸四边形ABCD中,P为AB边的中点,△ADP∽△PDC,判断四边形ABCD是否为邻等四边形;并证明你的结论;(3)、【拓展提升】
在平面直角坐标系中,AB为邻等四边形ABCD的邻等边,且AB边与x轴重合,已知A(-1,0),C(m,2 ),D(2,3),若在边AB上使∠DPC=∠BAD的点P有且仅有1个,请直接写出m的值.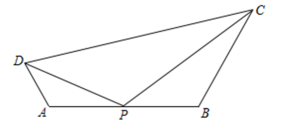 24. 如图,在平面直角坐标系xOy中,抛物线与两坐标轴分别相交于A,B,C三点,直线BC的函数解析式为y=kx+b;
24. 如图,在平面直角坐标系xOy中,抛物线与两坐标轴分别相交于A,B,C三点,直线BC的函数解析式为y=kx+b;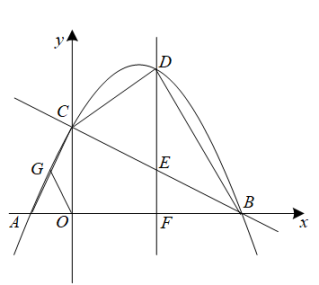 (1)、求点A、B、C的坐标;(2)、求出直线BC的函数解析式,并根据图像直接写出时x的取值范围;(3)、点D是第一象限内该抛物线上的动点,过点D作x轴的垂线交BC于点E,交x轴于点F.
(1)、求点A、B、C的坐标;(2)、求出直线BC的函数解析式,并根据图像直接写出时x的取值范围;(3)、点D是第一象限内该抛物线上的动点,过点D作x轴的垂线交BC于点E,交x轴于点F.①求△BCD面积的最大值;
②点G是AC的中点,若以点C,D,E为顶点的三角形与△AOG相似,求点D的坐标.