浙江省台州市仙居县两校联考2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程x²=3x的解为（）

A、x=3 B、x=0 C、x₁=0，x₂=﹣3 D、x₁=0，x₂=3

查看试题解析
3. 平面内有两点P，O，⊙O的半径为5，若PO＝4，则点P与⊙O的位置关系是（　　）

A、点P在⊙O外 B、点P在⊙O上 C、点P在⊙O内 D、无法判断

查看试题解析
4. 若关于x的一元二次方程kx²﹣2x+1＝0有两个不相等的实数根，则实数k的取值范围是（）

A、k＞1 B、k＜1 C、k＞1且k≠0 D、k＜1且k≠0

查看试题解析
5.
如图，已知圆心角∠AOB的度数为100°，则圆周角∠ACB的度数是（）

A、80° B、100° C、120° D、130°

查看试题解析
6. 将抛物线y＝x²﹣4x﹣4向右平移3个单位，再向上平移2个单位，所得抛物线的解析式是（　　）

A、y＝（x﹣5）²﹣6 B、y＝（x+1）²﹣6 C、y＝（x﹣5）²﹣10 D、y＝（x+1）²﹣5

查看试题解析
7. ⊙O的半径为5，弦 $A B ∥ C D$ ， AB＝6，CD＝8，则AB与CD距离为（　　）

A、7 B、8 C、7或1 D、1

查看试题解析
8. 西宁中心广场有各种音乐喷泉，其中一个喷水管喷水的最大高度为3米，此时距喷水管的水平距离为 $\frac{1}{2}$ 米，在如图所示的坐标系中，这个喷泉的函数关系式是（）

A、y＝－(x－ $\frac{1}{2}$ )²＋3 B、y＝－3(x+ $\frac{1}{2}$ )²+3 C、y＝－12(x- $\frac{1}{2}$ )²＋3 D、y＝－12(x+ $\frac{1}{2}$ )²+3

查看试题解析
9. 把一副三角板（如图甲）放置，其中∠ACB＝∠DEC＝90°，∠A＝45°，∠D＝30°，斜边AB＝6 $\sqrt{2}$ cm，DC＝ $8 \sqrt{2}$ cm，把三角板DCE绕点C顺时针旋转15°得到△D₁CE₁（如图乙），这时AB与CD₁相交于点O，与D₁E₁相交于点F，则线段AD₁的长为（　　）

A、5 $\sqrt{3}$ cm B、5 $\sqrt{2}$ cm C、17 $\sqrt{2}$ cm D、 $2 \sqrt{17}$ cm

查看试题解析
10. 若二次函数y＝﹣x²+mx在﹣2≤x≤1时的最大值为3，那么m的值是（　　）

A、2 $\sqrt{3}$ 或﹣4 B、﹣2 $\sqrt{3}$ 或4 C、﹣ $\frac{7}{2}$ 或2 $\sqrt{3}$ D、 $\frac{7}{2}$ 或﹣2 $\sqrt{3}$

查看试题解析

二、填空题

11. 已知﹣1是方程x²+bx﹣3＝0的一个根，则另一个根是．

查看试题解析
12. 有x支球队参加篮球比赛，共比赛21场，每两个队之间只比赛一场，则关于x的方程是．

查看试题解析
13. 如图，AB为⊙O的直径，C为⊙O外一点，过C作⊙O的切线，切点为B，连接AC交⊙O于点D，∠C＝42°．点E在AB右侧的半圆周上运动（不与A，B重合），则∠AED的度数为．

查看试题解析
14. 若点M(﹣1，y₁)，N(1，y₂)，P( $\frac{7}{2}$ ， y₃)都在抛物线y＝﹣ax²+4ax+a²+1（a＞0）上，则y₁ ， y₂ ， y₃大小关系是（用＜号连接）．

查看试题解析
15. 已知在△ABC中，∠C＝90°，AC＝12，BC＝5，在平面内将△ABC绕B点旋转，点A落到A′，点C落到C′，若旋转后点C的对应点C′落直线AB上，那么AA′的长为．

查看试题解析
16. 如图，用三个边长为2的正方形组成一个轴对称图形，则能将三个正方形完全覆盖的圆的最小半径是．

查看试题解析

三、解答题

17. 解下列方程：

(1)、x²+4x+3＝0；

(2)、3x²﹣x﹣1＝0．

查看试题解析
18. 如图，在平面直角坐标系中，△ABC的三个顶点分别为A（﹣1，﹣1）、B（﹣3，3）、C（﹣4，1）

（1）画出△ABC关于y轴对称的△A₁B₁C₁ ，并写出点B的对应点B₁的坐标；
（2）画出△ABC绕点A按顺时针旋转90°后的△AB₂C₂ ，并写出点C的对应点C₂的坐标．

查看试题解析
19. 二次函数y＝ax²+bx+c的图象过A（2，0），B（0，﹣1）和C（4，5）三点.

(1)、求二次函数的解析式；

(2)、设二次函数的图象与x轴的另一个交点为D，求点D的坐标.

查看试题解析
20. 如图，点A、B、C分别是⊙O上的点，∠B＝60°，CD是⊙O的直径，CD＝4 $\sqrt{3}$ ， P是CD延长线上的一点，且AP＝AC．

(1)、求证：AP是⊙O的切线；

(2)、求PD的长．

查看试题解析
21. 如图，小球从斜面顶端由静止开始沿斜面滚下，速度每秒增加1.6m．

(1)、写出小球滚动的距离s（单位：m）关于滚动的时间t（单位：s）的函数解析式．（提示：本题中，距离＝平均速度 $\bar{v}$ ×时间t， $\bar{v}$ ＝ $\frac{v_{0} + v_{t}}{2}$ ，其中，v₀是开始时的速度，vt是t秒时的速度．）

(2)、如果斜面的长是4m，小球从斜面顶端滚到底端用多长时间？

查看试题解析
22. 如图，AB，BC，CD分别与⊙O相切于点E，F，G，且AB∥CD，BO＝6cm，CO＝8cm.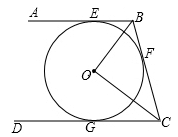

(1)、求BC的长；

(2)、求⊙O的半径长.

查看试题解析
23. 某超市准备销售一种儿童玩具，进货价格为每件40元，并且每件的售价不低于进货价．经过市场调查，每月的销售量y（件）与每件的售价x（元）之间满足如图所示的函数关系．

(1)、求每月的销售量y（件）与每件的售价x（元）之间的函数关系式；（不必写出自变量的取值范围）

(2)、物价部门规定，该儿童玩具每件的利润不允许高于进货价的60%．设销售这种儿童玩具每月的总利润为w（元），那么每件售价定为多少元可获得最大利润？最大利润是多少？

查看试题解析
24. 如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的矩形CEFD拼在一起，构成一个大的矩形ABEF．现将小矩形CEFD绕点C顺时针旋转至CE′F′D′，旋转角为α．

(1)、当点D′恰好落在EF边上时，旋转角α＝°；

(2)、如图2，G为BC中点，且0°＜α＜90°，求证：GD′＝DE′；

(3)、小矩形CEFD绕点C顺时针旋转一周的过程中，△DCD′与△CBD′能否全等？若能，直接写出旋转角α的值，若不能，说明理由．

查看试题解析