浙江省宁波市镇海区2020-2021学年九年级上学期期中数学试题
试卷更新日期:2022-09-14 类型:期中考试
一、单选题
-
1. 抛物线y=4x2﹣3的顶点坐标是( )A、(0,3) B、(0,﹣3) C、(﹣3,0) D、(4,﹣3)2. 下列关于事件发生可能性的表述,正确的是( )A、事件:“在地面,向上抛石子后落在地上”,该事件是随机事件 B、体育彩票的中奖率为10%,则买100张彩票必有10张中奖 C、在同批次10000件产品中抽取100件发现有5件次品,则这批产品中大约有500件左右的次品 D、掷两枚硬币,朝上的一面是一正面一反面的概率为3. 如图, , , 为圆上的三点, , 点可能是圆心的是( )A、
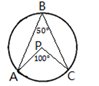 B、
B、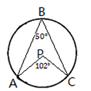 C、
C、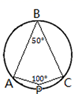 D、
D、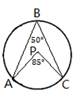 4. 把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、5. 如图所示,P是等边三角形ABC内的一点,若将三角形PBC绕点B旋转到三角形P′BA,则∠P′BP的度数为( )
4. 把函数 的图象向右平移1个单位长度,平移后图象的函数解析式为( )A、 B、 C、 D、5. 如图所示,P是等边三角形ABC内的一点,若将三角形PBC绕点B旋转到三角形P′BA,则∠P′BP的度数为( )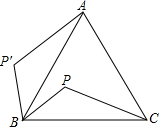 A、45° B、60° C、90° D、120°6. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、7. 圆内接四边形ABCD的四个内角之比可能是( )A、1:2:3:4 B、1:3:4:5 C、2:3:4:5 D、2:3:5:48. 已知M(1,2),N(3,﹣3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(﹣3,5) C、(1,2) D、(1,﹣2)9. 如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )
A、45° B、60° C、90° D、120°6. 已知(﹣3, ),(﹣2, ),(1, )是抛物线 上的点,则( )A、 B、 C、 D、7. 圆内接四边形ABCD的四个内角之比可能是( )A、1:2:3:4 B、1:3:4:5 C、2:3:4:5 D、2:3:5:48. 已知M(1,2),N(3,﹣3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(﹣3,5) C、(1,2) D、(1,﹣2)9. 如图,将边长为6的正六边形铁丝框ABCDEF(面积记为S1)变形为以点D为圆心,CD为半径的扇形(面积记为S2),则S1与S2的关系为( )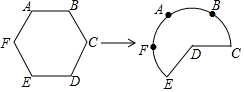 A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S210. 三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( )
A、S1= S2 B、S1<S2 C、S1=S2 D、S1>S210. 三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小完全相同.当水面刚好淹没小孔时,大孔水面宽度为10米,孔顶离水面1.5米;当水位下降,大孔水面宽度为14米时,单个小孔的水面宽度为4米,若大孔水面宽度为20米,则单个小孔的水面宽度为( ) A、4 米 B、5 米 C、2 米 D、7米
A、4 米 B、5 米 C、2 米 D、7米二、填空题
-
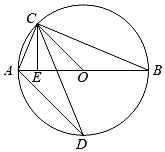
11. 从 中任取一数作为 ,使抛物线 的开口向上的概率为 .12. 已知⊙O的半径为5,若P到圆心O的距离是4,则点P与⊙O的位置关系是 .13. 若二次函数 的图象与x轴有两个交点,则k的取值范围是.14. 一条弦所对的圆心角的度数为95°,这条弦所对的圆周角的度数为.15. 二次函数 (其中m>0),下列命题:①该图象过点(6,0);②该二次函数顶点在第三象限;③当x>3时,y随x的增大而增大;④若当x<n时,都有y随x的增大而减小,则 .正确的序号是.16. 如图,AB为⊙O的直径,且AB=10,点C为⊙O上的一点,CE⊥AB于点E,∠OCE的角平分线交⊙O于点D,弦AC=6,那么△ACD的面积是 .
三、解答题
-
17. 城市小区生活垃圾分为干垃圾、湿垃圾、有害垃圾和可回收垃圾四种不同的类型.(1)、甲投放了一袋垃圾,恰好是湿垃圾的概率是 .(2)、甲、乙分别投放了一袋垃圾,通过画树状图或列表求恰好是同一类型垃圾的概率.18. 如图,△ABC内接于⊙O,设∠B=α,请用无刻度的直尺按要求作图(保留作图痕迹).
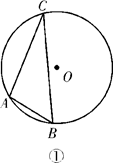
 (1)、在图①中画一个度数是2α的圆心角(2)、在图②中作出∠C的余角.19. 已知二次函数的图象经过点 和点 ,且有最小值为 .(1)、求这个函数的解析式;(2)、函数的开口方向、对称轴;(3)、当 时, 的取值范围.20. 已知:如图,在⊙O中,AB=CD,AB与CD相交于点M,
(1)、在图①中画一个度数是2α的圆心角(2)、在图②中作出∠C的余角.19. 已知二次函数的图象经过点 和点 ,且有最小值为 .(1)、求这个函数的解析式;(2)、函数的开口方向、对称轴;(3)、当 时, 的取值范围.20. 已知:如图,在⊙O中,AB=CD,AB与CD相交于点M,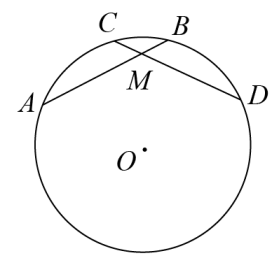 (1)、求证:;(2)、求证:AM=DM.21. 如图,已知A、B、C是上三点,其中 , 过点B画于点D.
(1)、求证:;(2)、求证:AM=DM.21. 如图,已知A、B、C是上三点,其中 , 过点B画于点D.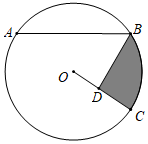 (1)、求证:;(2)、若 , 求图中阴影部分的面积.22. 某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间t(天)之间的函数关系为p= , 且t为整数,日销售量y(千克)与时间t(天)之间的函数关系如图所示.
(1)、求证:;(2)、若 , 求图中阴影部分的面积.22. 某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间t(天)之间的函数关系为p= , 且t为整数,日销售量y(千克)与时间t(天)之间的函数关系如图所示. (1)、求日销售量y与时间t的函数表达式.(2)、哪一天的日销售利润最大?最大利润是多少?23. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答:
(1)、求日销售量y与时间t的函数表达式.(2)、哪一天的日销售利润最大?最大利润是多少?23. 若一个四边形的两条对角线互相垂直且相等,则称这个四边形为“奇妙四边形”.如图1,四边形ABCD中,若AC=BD,AC⊥BD,则称四边形ABCD为奇妙四边形.根据“奇妙四边形”对角线互相垂直的特征可得“奇妙四边形”的一个重要性质:“奇妙四边形”的面积等于两条对角线乘积的一半.根据以上信息回答: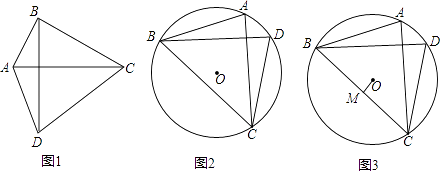 (1)、矩形 “奇妙四边形”(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;(3)、如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.24. 如图,抛物线y=﹣与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)、矩形 “奇妙四边形”(填“是”或“不是”);(2)、如图2,已知⊙O的内接四边形ABCD是“奇妙四边形”,若⊙O的半径为6,∠BCD=60°.求“奇妙四边形”ABCD的面积;(3)、如图3,已知⊙O的内接四边形ABCD是“奇妙四边形”作OM⊥BC于M.请猜测OM与AD的数量关系,并证明你的结论.24. 如图,抛物线y=﹣与x轴交于点A,点B,与y轴交于点C,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q. (1)、求点A、点B、点C的坐标;(2)、求直线BD的解析式;(3)、当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(4)、在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、求点A、点B、点C的坐标;(2)、求直线BD的解析式;(3)、当点P在线段OB上运动时,直线l交BD于点M,试探究m为何值时,四边形CQMD是平行四边形;(4)、在点P的运动过程中,是否存在点Q,使△BDQ是以BD为直角边的直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.