浙江省宁波市慈溪市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 二次函数y＝－2（x－3）²＋4的顶点坐标是（）

A、（－3，4） B、（3，4） C、（3，－4） D、（－3，－4）

查看试题解析
2. 下列事件中，是必然事件的是（）

A、抛掷一枚硬币正面向上 B、从一副完整扑克牌中任抽一张，恰好抽到红桃A C、今天太阳从西边升起 D、从4件红衣服和2件黑衣服中任抽3件有红衣服

查看试题解析
3. 如图，点A，B，C在⊙O上，∠ACB＝37°，则∠AOB的度数是（）

A、73° B、74° C、64° D、37°

查看试题解析
4. 已知点A（－3，y₁），B（0，y₂），C（3，y₃）都在二次函数y＝－（x＋2）²＋4的图象上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₃＜y₂＜y₁ B、y₁＝y₃＜y₂ C、y₁＜y₂＜y₃ D、y₁＜y₃＜y₂

查看试题解析
5. 下列语句中，正确的是（）

A、长度相等的两条弧是等弧 B、相等的圆周角所对的弧相等 C、平分弦的直径垂直于弦 D、相等的弧所对的圆心角相等

查看试题解析
6. 下列二次函数的图象与x轴没有交点的是（）

A、y＝－3x²＋2x B、y＝x²－3x－4 C、y＝x²－4x＋4 D、y＝x²＋4x＋5

查看试题解析
7. ⊙O的半径为5，M是圆外一点，MO＝6，∠OMA＝30°，则弦AB的长为（　　）

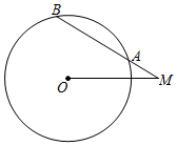A、4 B、6 C、6 $\sqrt{3}$ D、8

查看试题解析
8. 如图，在方格纸中，随机选择标有序号①②③④⑤⑥中的一个小正方形涂黑，与图中的阴影部分构成轴对称图形的概率是（　　）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{2}{3}$ D、 $\frac{1}{6}$

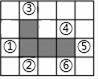查看试题解析
9. 如图，二次函数y＝ax²＋bx＋c（a＞0）的图象与x轴交于A，B两点，与y轴正半轴交于点C，它的对称轴为直线x＝﹣1.则下列选项中正确的是（）

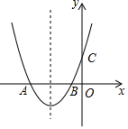A、abc＜0 B、4ac﹣b²＞0 C、c﹣a＜0 D、 $b < 2 c$

查看试题解析
10. 如图，用6个小正方形构造如图所示的网格图（每个小正方形的边长均为2），设经过图中M、P、H三点的圆弧与AH交于R，则图中阴影部分面积（）

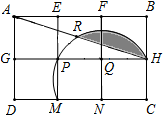A、 $\frac{5}{4}$ π﹣ $\frac{5}{2}$ B、 $\frac{5}{2}$ π﹣5 C、2π﹣5 D、3π﹣2

查看试题解析

二、填空题

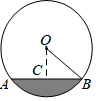
11. 二次函数 $y = 2 x^{2} - 4 x + 1$ 的图象开口方向：，对称轴为．

查看试题解析
12. 粉笔盒中有10支白色粉笔盒若干支彩色粉笔，每支粉笔除颜色外均相同，从中随机拿一支粉笔，拿到白色的概率为 $\frac{2}{5}$ ，则其中彩色粉笔的数量为支．

查看试题解析
13. 一根排水管的截面如图所示，已知排水管的半径OB＝5cm，水面宽AB＝8cm，则截面圆心O到水面的距离OC的长是．

查看试题解析
14. 函数 $y = x^{2} - 2 x + 3$ 的图象经过向左平移2个单位，向下平移1个单位，得到的新函数表达式为．

查看试题解析
15. 一条弦分圆周为4∶6，则这条弦所对的圆周角的度数为．

查看试题解析
16. 如图，在以AB为直径的半圆O中，C是半圆的三等分点，点P是弧BC上一动点，连接CP，AP，作OM垂直CP交AP于N，连接BN，若AB＝12，则NB的最小值是．

查看试题解析

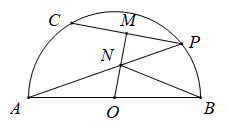
三、解答题

17. 已知二次函数的图象经过（－6，0），（2，0），（0，－6）三点．

(1)、求这个二次函数的表达式；

(2)、求这个二次函数的顶点坐标．

查看试题解析
18. 如图，在Rt△ABC中，∠C＝90°．

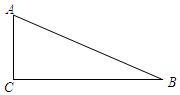(1)、请用无刻度直尺和圆规画出Rt△ABC的外接圆；（不写作法，保留作图）

(2)、若AC＝5，BC＝12，求Rt△ABC的外接圆的面积．

查看试题解析
19. 城市小区生活垃圾分为干垃圾、湿垃圾、有害垃圾和可回收垃圾四种不同的类型．

(1)、甲投放了一袋垃圾，恰好是湿垃圾的概率是．

(2)、甲、乙分别投放了一袋垃圾，通过画树状图或列表求恰好是同一类型垃圾的概率．

查看试题解析
20. 如图，A，B，C是⊙O上的点，其中 $\overset{⌢}{A B} = 2 \overset{⌢}{B C}$ ，过点B画BD⊥OC于点D．

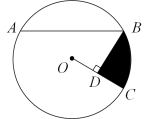(1)、求证：AB＝2BD．

(2)、若AB＝ $4 \sqrt{3}$ ， CD＝2，求 $\overset{⌢}{B C}$ 的长和图中涂色部分的面积．

查看试题解析
21. 某经销商销售一种成本价为100元/件的商品，已知销售价不低于成本价，且物价部门规定这种产品的销售价不得高于180元/件．在销售过程中发现销量y（kg）与售价x（元/kg）之间满足一次函数关系，对应关系如下表所示：
x
120
140
150
170
y
360
320
300
260

(1)、求y与x之间的函数表达式，并写出自变量x的取值范围．

(2)、设销售这种商品每天所获得的利润为W元，求W与x之间的函数表达式；该商品销售单价定为多少元时，才能使经销商所获利润最大？最大利润是多少？

查看试题解析
22. 如图，有一座圆弧形拱桥，桥下水面宽度AB为12m，拱高CD为4m．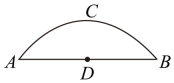

(1)、求拱桥的半径．

(2)、有一艘宽为7.8m的货船，船舱顶部为长方形，并高出水面3m，则此货船是否能顺利通过此圆弧形拱桥？并说明理由．

查看试题解析
23. 如图，抛物线 $y = - x^{2} + b x + c$ 的图象与x轴正半轴交于点A（3，0），与y轴交于点B（0，3）直线l的函数表达式为 $y = - x + 6$ ，

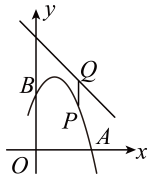(1)、求抛物线的函数表达式；

(2)、动点P在抛物线AB段上运动，经过点P作y轴的平行线交直线l于点Q，求线段PQ的取值范围．

查看试题解析
24. 如图1，在⊙O中，弦AD平分圆周角∠BAC，我们将圆中以A为公共点的三条弦BA，CA，DA构成的图形称为圆中“爪形A”，弦BA，CA，DA称为“爪形A”的爪．

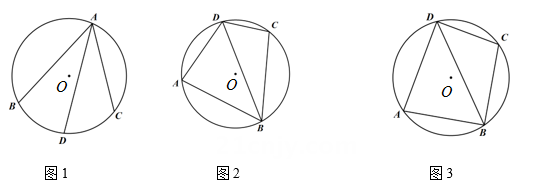(1)、如图2，四边形ABCD内接于圆，AB＝BC，
①证明：圆中存在“爪形D”；
②若∠ADC＝120°，求证：AD＋CD＝BD

(2)、如图3，四边形ABCD内接于圆，其中BA＝BC，连接BD．若AD⊥DC，此时“爪形D”的爪之间满足怎样的数量关系，请直接写出结果．

查看试题解析

x	120	140	150	170
y	360	320	300	260