浙江省金华市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 已知函数y＝（m＋3）x²＋4是二次函数，则m的取值范围为（）

A、m＞－3 B、m＜－3 C、m≠－3 D、任意实数

查看试题解析
2. 下列事件中，是随机事件的是（）

A、三角形中任意两边之和大于第三边 B、太阳从东方升起 C、车辆随机到达一个路口，遇到绿灯 D、一个有理数的绝对值为负数

查看试题解析
3. 已知圆心角为120°的扇形的面积为12π，则扇形的半径为（）

A、4 B、6 C、 $4 \sqrt{3}$ D、 $6 \sqrt{2}$

查看试题解析
4. 某轨道列车共有3节车厢，设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车，则甲和乙从同一节车厢上车的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{2}$

查看试题解析
5. 下列命题中正确的有（）
①平分弦的直径垂直于这条弦；②相等的圆心角所对的弧相等；③相等的弧所对的弦相等；④相等的弦所对的圆心角相等；⑤弦心距相等，则所对的弦相等；⑥直径所对的圆周角为直角．

A、1个 B、2个 C、5个 D、6个

查看试题解析
6. 如图，MN是 $⊙ O$ 的直径，点A是半圆上一个三等分点，点B是 $\overset{⌢}{A N}$ 的中点，点 $B^{'}$ 是点B关于MN的对称点， $⊙ O$ 的半径为1，则 $A B^{'}$ 的长等于（）

A、1 B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $2$

查看试题解析
7. 如图，△ABC中，∠C=63°，将△ABC绕点A顺时针旋转后，得到△AB′C′，且C′在边BC上，则∠B′C′B的度数为（）

A、45° B、54° C、87° D、70°

查看试题解析
8. 如图，在扇形AOB中∠AOB=90°，正方形CDEF的顶点C是 $\overset{⌢}{A B}$ 的中点，点D在OB上，点E在OB的延长线上，当正方形CDEF的边长为2 $\sqrt{2}$ 时，则阴影部分的面积为（）

A、2π﹣4 B、4π﹣8 C、2π﹣8 D、4π﹣4

查看试题解析
9. 如图， $△ A B C$ 的边 $A B$ 在x轴上，边 $A C$ 交y轴于点E， $A E ： E C = 1 ： 2$ ，反比例函数 $y = \frac{k}{x}$ 过C点，且交线段 $B C$ 于D， $B D ： D C = 1 ： 3$ ，连接 $A D$ ，若 $S_{△ A B D} = \frac{11}{4}$ ，则k的值为（）

A、 $\frac{11}{2}$ B、 $\frac{33}{4}$ C、4 D、6

查看试题解析
10. 点A ， B的坐标分别为A (4，0)，B(0，4)，点C为坐标平面内一点，BC﹦2，点M为线段AC的中点，连接OM ，则OM的最大值为（）

A、2 $\sqrt{2}$ ＋1 B、2 $\sqrt{2}$ ＋2 C、4 $\sqrt{2}$ ＋1 D、4 $\sqrt{2}$ -2

查看试题解析

二、填空题

11. 分解因式： $2 x^{3} + 4 x^{2} + 2 x =$ ．

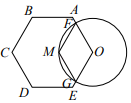
查看试题解析
12. 已知圆O的面积为 $25 π$ ，若点P在圆上，则 $P O =$ ．

查看试题解析
13. 如图，⊙O与正六边形OABCDE的边OA，OE分别交于点F，G，点M为劣弧FG的中点.若FM＝ $4 \sqrt{2}$ ，则点O到FM的距离是 .

查看试题解析
14. 如图，在Rt $△$ ABC中，∠ACB＝90°，AB＝ $\sqrt{5}$ ，BC＝2，以点A为圆心，AC的长为半径画弧，交AB于点D，交AC于点C，以点B为圆心，AC的长为半径画弧，交AB于点E，交BC于点F，则图中阴影部分的面积为 .

查看试题解析
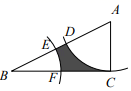15. 如图所示，在平面直角坐标系xOy中，点P是钝角 $△ A B C$ 的外心，点A、B、P的坐标分别为 $(1 ， 0)$ ， $(2 ， 5)$ ， $(4 ， 2)$ ，若第一象限的点C横坐标、纵坐标均为整数，则点C的坐标为．

查看试题解析
16. 如图，在△ABC中，∠BAC＝30°，∠ACB＝45°，AB＝2，点P从点A出发沿AB方向运动，到达点B时停止运动，连结CP ，点A关于直线CP的对称点为A′，连结A′C ， A′P ．在运动过程中，点A′到直线AB距离的最大值是；点P到达点B时，线段A′P扫过的面积为．

查看试题解析

三、解答题

17.

(1)、计算： ${(- 1)}^{2021} - \sqrt{9} + {(\frac{1}{2})}^{- 1} + {(π - 3.14)}^{0}$

(2)、解方程： $\frac{4 x}{x - 2} - 1 = \frac{3}{2 - x}$

查看试题解析
18. 在一次篮球拓展课上， $A$ ， $B$ ， $C$ 三人玩篮球传球游戏，游戏规则是：每一次传球由三人中的一位将球随机地传给另外两人中的某一人.例如：第一次由 $A$ 传球，则 $A$ 将球随机地传给 $B$ ， $C$ 两人中的某一人.

(1)、若第一次由 $A$ 传球，求两次传球后，球恰好回到 $A$ 手中的概率.（要求用画树状图法或列表法）

(2)、从 $A$ ， $B$ ， $C$ 三人中随机选择一人开始进行传球，求两次传球后，球恰好在 $A$ 手中的概率.（要求用画树状图法或列表法）

查看试题解析
19. 如图所示，已知AB是 $⊙ O$ 的直径，C，D是 $⊙ O$ 上的点， $O C ∥ B D$ ，交AD于点E，连结BC．

(1)、求证： $A E = E D$ ；

(2)、若 $A B = 10$ ， $∠ A B C = 36 °$ ，求 $\overset{⌢}{A C}$ 的长．

查看试题解析
20. 某游乐场的圆形喷水池中心O有一雕塑OA，从A点向四周喷水，喷出的水柱为抛物线，且形状相同.如图，以水平方向为x轴，点O为原点建立直角坐标系，点A在y轴上，x轴上的点C，D为水柱的落水点，水柱所在抛物线第一象限部分的函数表达式为 $y = - \frac{1}{6} {(x - 5)}^{2} + 6$ .

(1)、求雕塑高OA.

(2)、求落水点C，D之间的距离.

(3)、若需要在OD上的点E处竖立雕塑EF， $O E = 10 m$ ， $E F = 1.8 m ， E F ⊥ O D$ .问：顶部F是否会碰到水柱？请通过计算说明.

查看试题解析
21. 已知某品牌床单进价为每件60元，每月的销量w（件）与售价x（元）的相关信息如下表（符合一次函数关系）：
售价（元/件）
100
110
120
130
…
月销售量（件）
200
180
160
140
…

(1)、销售该品牌床单每件的利润是元（用含x的式子表示）．

(2)、用含x的代数式表示月销量w．

(3)、设销售该品牌床单的月利润为y元，那么售价为多少时，当月的利润最大，最大利润是多少？

查看试题解析
22. 矩形ABCD中，点E为BC上一点， $B E = \frac{1}{4} B C$ ，点F为边AD上的一个动点．连结EF，将矩形ABCD沿着EF翻折，使点C恰好落在AB上，其对应点为M．

(1)、如图1所示，当点M与点A重合时，求证： $△ A E F$ 是等腰三角形；

(2)、如图2所示，当点F与点D重合时，求 $\frac{B C}{A B}$ 的值；

(3)、在图3所示中，若 $\frac{D F}{A D} = \frac{1}{n}$ ，当 $\frac{B C}{A B} = \frac{6 \sqrt{2}}{7}$ 时，求n的值．

查看试题解析
23. 如图所示，直线y=x-3与x轴交于点B，与y轴交于点C，抛物线y=x²+bx+c 经过B，C两点，与x轴另一交点为A．点P以每秒 $\sqrt{2}$ 个单位长度的速度在线段BC上由点B向点C运动（点P不与点B和点C重合），设运动时间为t秒，过点P作x轴垂线交x轴于点D，交抛物线于点E，连结AE交BC于点Q．

(1)、求抛物线的解析式；

(2)、当 $\frac{E Q}{A Q} = \frac{1}{2}$ 时求t的值．

查看试题解析
24. 如图，已知抛物线 $y = a x^{2} + b x + 4$ 经过 $A (- 1 ， 0)$ ， $B (4 ， 0)$ 两点，交y轴于点C．

(1)、求抛物线的解析式；

(2)、连接 $B C$ ，求直线 $B C$ 的解析式；

(3)、请在抛物线的对称轴上找一点P，使 $A P + P C$ 的值最小，求点P的坐标，并求出此时 $A P + P C$ 的最小值；

(4)、点M为x轴上一动点，在抛物线上是否存在一点N，使得以A、C、M、N四点为顶点的四边形是平行四边形？若存在，求出点N的坐标；若不存在，请说明理由．

查看试题解析

售价（元/件）	100	110	120	130	…
月销售量（件）	200	180	160	140	…