浙江省杭州市拱墅区锦绣育才教育集团2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 已知圆的半径为2cm，一点到圆心的距离是3cm，则这点在（）

A、圆外 B、圆上 C、圆内 D、不能确定

查看试题解析
2. 如图，已知A，B均为⊙O上一点，若∠AOB＝80°，则∠ACB＝（　　）

A、80° B、70° C、60° D、40°

查看试题解析
3. 不透明的袋子里装有7个只有颜色不同的球，其中3个黑球，4个白球，搅匀后任意摸出一个球，是白球的概率是（）

A、 $\frac{3}{4}$ B、 $\frac{3}{7}$ C、 $\frac{4}{7}$ D、 $\frac{4}{3}$

查看试题解析
4. 如果2a＝5b ，那么下列比例式中正确的是（）

A、 $\frac{a}{b} = \frac{2}{5}$ B、 $\frac{a}{5} = \frac{2}{b}$ C、 $\frac{a}{b} = \frac{5}{2}$ D、 $\frac{a}{2} = \frac{b}{5}$

查看试题解析
5. 抛物线y＝x²向左平移3个单位，再向下平移2个单位后，所得的抛物线表达式是（　　）

A、y＝（x﹣3）²﹣2 B、y＝（x﹣3）²+2 C、y＝（x+3）²﹣2 D、y＝（x+3）²+2

查看试题解析
6. 如图，已知 $△ A D E ∼ △ A C B$ ，若AB=10，AC=8，AD=4，则AE的长是（）

A、4 B、3.2 C、20 D、5

查看试题解析
7. 已知点A（3，y₁），B（4，y₂），C（﹣3，y₃）均在抛物线 $y = \frac{1}{2} x^{2} - 2 x + m$ 上，下列说法中正确的是（）

A、 $y_{3} < y_{2} < y_{1}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{2} < y_{1} < y_{3}$

查看试题解析
8. 筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图1，筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2，已知圆心O在水面上方，且 $⊙ O$ 被水面截得的弦 $A B$ 长为6米， $⊙ O$ 半径长为4米.若点C为运行轨道的最低点，则点C到弦 $A B$ 所在直线的距离是（）

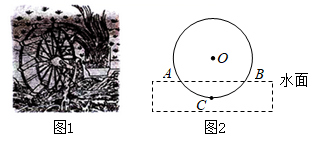A、1米 B、 $(4 - \sqrt{7})$ 米 C、2米 D、 $(4 + \sqrt{7})$ 米

查看试题解析
9. 二次函数y＝ax²＋bx＋1（a≠0）的图象的顶点在第一象限，且过点（﹣1，0）．设t＝a＋b＋1，则t值的变化范围是（）

A、0＜t＜1 B、0＜t＜2 C、1＜t＜2 D、﹣1＜t＜1

查看试题解析
10. 如图，H是△ABC的重心，延长AH交BC于D，延长BH交AC于M，E是DC上一点，且DE∶EC＝5∶2，连结AE交BM于G，则BH∶HG∶GM等于（）

A、7∶5∶2 B、13∶5∶2 C、5∶3∶1 D、26∶10∶3

查看试题解析

二、填空题

11. 二次函数y＝（x﹣1）²＋3图象的顶点坐标是．

查看试题解析
12. 已知圆的半径为2，则60°圆心角所对的弧长为．

查看试题解析
13. 已知S＝t²﹣2t﹣15，则S的最小值为．

查看试题解析
14. 已知一个正多边形内角的度数为108°，则它的边数为．

查看试题解析
15. 如图，已知△ABC内接于⊙O，AB＝AC，∠BAC＝36°，连结BO并延长，交⊙O于D，则∠ACD＝度.

查看试题解析
16. 一个球从地面竖直向上弹起时的速度为10m/s，经过t（s）时球的高度为h（m）．已知物体竖直运动中， $h = v_{0} t - \frac{1}{2} g t^{2}$ （v₀表示物体运动上弹开始时的速度，g表示重力系数，取g＝10m/s²）．则球从弹起至回到地面的过程中，前后两次高度达到3.75m的时间间隔为s．

查看试题解析

三、解答题

17. 全面两孩政策实施后，甲、乙两个家庭有了各自的规划，假定生男生女的概率相同，回答下列问题：

(1)、甲家庭已有一个男孩，准备再生一个孩子，则第二个孩子是女孩的概率是；

(2)、乙家庭没有孩子，准备生两个孩子，求至少有一个孩子是女孩的概率．

查看试题解析
18.

(1)、已知 $\frac{a}{b} = \frac{3}{5}$ ，求 $\frac{a + b}{b}$ 的值；

(2)、已知点P是线段AB的黄金分割点，PA＞PB，AB=2，求PA、PB的长．

查看试题解析
19. 如图，半圆O的直径AB=20，将半圆O绕点B顺针旋转45°得到半圆O′，与AB交于点P．

(1)、求AP的长；

(2)、求图中阴影部分的面积（结果保留π）．

查看试题解析
20. 某单位为了创建城市文明单位，准备在单位的墙（线段MN所示）外开辟一处长方形的土地进行绿化美化，除墙体外三面要用栅栏围起来，计划用栅栏40米．

(1)、不考虑墙体长度，问长方形的各边的长为多少米时，长方形的面积最大？

(2)、若11≤AB≤12，试求长方形面积S的取值范围．

查看试题解析
21. 如图，四边形ABCD内接于⊙O，点E在CB的延长线上，BA平分∠EBD，AE＝AB．

(1)、求证：AC＝AD；

(2)、求证：△AEB∽△ACD；

(3)、当 $\frac{A E}{E B} = \frac{3}{2}$ ， AD＝6时，求CD的长．

查看试题解析
22. 在平面直角坐标系xOy中，A（1，m）和B（3，n）在抛物线y＝ax²＋bx（a＞0）上．

(1)、若m＝3，n＝15，求该抛物线的解析式；

(2)、若A、B两点关于对称轴对称，点（﹣1，y₁），（1，y₂），（4，y₃）在该抛物线上，比较y₁ ， y₂ ， y₃的大小，并说明理由．

(3)、若该抛物线的对称轴为x＝﹣1，求m，n满足的等量关系．

查看试题解析
23.
如图，已知⊙O的半径长为1，AB、AC是⊙O的两条弦，且AB=AC，BO的延长线交AC于点D，联结OA、OC．

(1)、求证：△OAD∽△ABD；

(2)、当△OCD是直角三角形时，求B、C两点的距离；

(3)、记△AOB、△AOD、△COD 的面积分别为S₁、S₂、S₃ ，如果S₂是S₁和S₃的比例中项，求OD的长．

查看试题解析