湖北省黄石市2022年中考数学试卷
试卷更新日期:2022-09-14 类型:中考真卷
一、单选题
-
1. 的绝对值是( )A、 B、 C、 D、2. 下面四幅图是我国一些博物馆的标志,其中既是轴对称图形又是中心对称图形的是( )A、温州博物馆
 B、西藏博物馆
B、西藏博物馆 C、广东博物馆
C、广东博物馆 D、湖北博物馆
D、湖北博物馆 3. 由5个大小相同的小正方体搭成的几何体如图所示,它的主视图是( )
3. 由5个大小相同的小正方体搭成的几何体如图所示,它的主视图是( )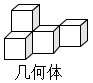 A、
A、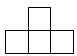 B、
B、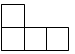 C、
C、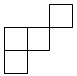 D、
D、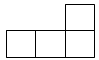 4. 下列运算正确的是( )A、 B、 C、 D、5. 函数的自变量x的取值范围是( )A、且 B、且 C、 D、且6. 我市某校开展共创文明班,一起向未来的古诗文朗诵比赛活动,有10位同学参加了初赛,按初赛成绩由高到低取前5位进入决赛.如果小王同学知道了自己的成绩后,要判断能否进入决赛,他需要知道这10位同学成绩的( )A、平均数 B、众数 C、中位数 D、方差7. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )
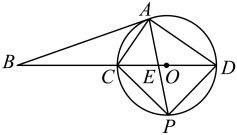
4. 下列运算正确的是( )A、 B、 C、 D、5. 函数的自变量x的取值范围是( )A、且 B、且 C、 D、且6. 我市某校开展共创文明班,一起向未来的古诗文朗诵比赛活动,有10位同学参加了初赛,按初赛成绩由高到低取前5位进入决赛.如果小王同学知道了自己的成绩后,要判断能否进入决赛,他需要知道这10位同学成绩的( )A、平均数 B、众数 C、中位数 D、方差7. 如图,正方形的边长为 , 将正方形绕原点O顺时针旋转45°,则点B的对应点的坐标为( )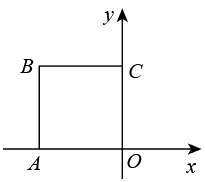 A、 B、 C、 D、8. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线 , 分别交线段 , 于点D,E,若 , 的周长为11 , 则的周长为( )
A、 B、 C、 D、8. 如图,在中,分别以A,C为圆心,大于长为半径作弧,两弧分别相交于M,N两点,作直线 , 分别交线段 , 于点D,E,若 , 的周长为11 , 则的周长为( )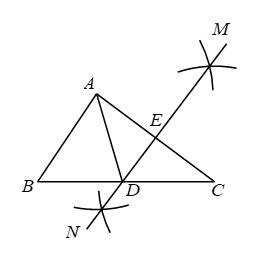 A、13 B、14 C、15 D、169. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )
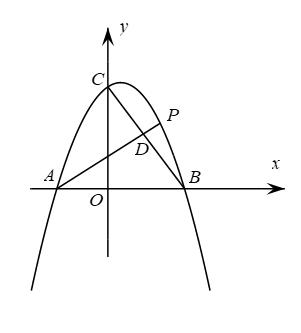
A、13 B、14 C、15 D、169. 我国魏晋时期的数学家刘徽首创割圆术:割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体,而无所失矣",即通过圆内接正多边形割圆,从正六边形开始,每次边数成倍增加,依次可得圆内接正十二边形,内接正二十四边形,…….边数越多割得越细,正多边形的周长就越接近圆的周长.再根据“圆周率等于圆周长与该圆直径的比”来计算圆周率.设圆的半径为R,图1中圆内接正六边形的周长 , 则 . 再利用圆的内接正十二边形来计算圆周率则圆周率约为( )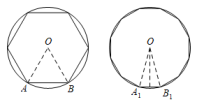 A、 B、 C、 D、10. 已知二次函数的部分图象如图所示,对称轴为直线 , 有以下结论:①;②若t为任意实数,则有;③当图象经过点时,方程的两根为 , (),则 , 其中,正确结论的个数是( )
A、 B、 C、 D、10. 已知二次函数的部分图象如图所示,对称轴为直线 , 有以下结论:①;②若t为任意实数,则有;③当图象经过点时,方程的两根为 , (),则 , 其中,正确结论的个数是( ) A、0 B、1 C、2 D、3
A、0 B、1 C、2 D、3二、填空题
-
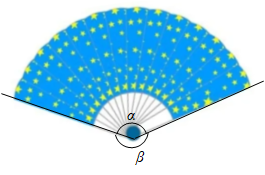
11. 计算: .12. 分解因式:x3y﹣9xy= .13. 据新华社2022年1月26日报道,2021年全年新增减税降费约1.1万亿元,有力支持国民经济持续稳定恢复用科学记数法表示1.1万亿元,可以表示为元.14. 如图,圆中扇子对应的圆心角()与剩余圆心角的比值为黄金比时,扇子会显得更加美观,若黄金比取0.6,则的度数是 .
 15. 已知关于x的方程的解为负数,则a的取值范围是 .16. 某校数学兴趣小组开展无人机测旗杆的活动:已知无人机的飞行高度为30m,当无人机飞行至A处时,观测旗杆顶部的俯角为30°,继续飞行20m到达B处,测得旗杆顶部的俯角为60°,则旗杆的高度约为m.(参考数据: , 结果按四舍五八保留一位小数)
15. 已知关于x的方程的解为负数,则a的取值范围是 .16. 某校数学兴趣小组开展无人机测旗杆的活动:已知无人机的飞行高度为30m,当无人机飞行至A处时,观测旗杆顶部的俯角为30°,继续飞行20m到达B处,测得旗杆顶部的俯角为60°,则旗杆的高度约为m.(参考数据: , 结果按四舍五八保留一位小数)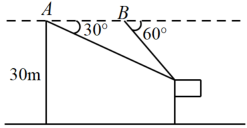 17. 如图,反比例函数的图象经过矩形对角线的交点E和点A,点B、C在x轴上,的面积为6,则 .
17. 如图,反比例函数的图象经过矩形对角线的交点E和点A,点B、C在x轴上,的面积为6,则 .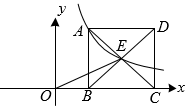
三、解答题
-
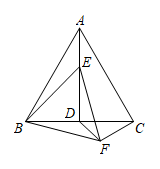
18. 如图,等边中, , 点E为高上的一动点,以为边作等边 , 连接 , , 则 , 的最小值为 .
 19. 先化简,再求值: , 从-3,-1,2中选择合适的a的值代入求值.20. 如图,在和中, , , , 且点D在线段上,连 .
19. 先化简,再求值: , 从-3,-1,2中选择合适的a的值代入求值.20. 如图,在和中, , , , 且点D在线段上,连 .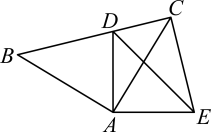 (1)、求证:;(2)、若 , 求的度数.21. 某中学为了解学生每学期诵读经典的情况,在全校范围内随机抽查了部分学生上一学期阅读量,学校将阅读量分成优秀、良好、较好、一般四个等级,绘制如下统计表:
(1)、求证:;(2)、若 , 求的度数.21. 某中学为了解学生每学期诵读经典的情况,在全校范围内随机抽查了部分学生上一学期阅读量,学校将阅读量分成优秀、良好、较好、一般四个等级,绘制如下统计表:等级
一般
较好
良好
优秀
阅读量/本
3
4
5
6
频数
12
a
14
4
频率
0.24
0.40
b
c
请根据统计表中提供的信息,解答下列问题:
(1)、本次调查一共随机抽取了名学生;表中 , , .(2)、求所抽查学生阅读量的众数和平均数.(3)、样本数据中优秀等级学生有4人,其中仅有1名男生.现从中任选派2名学生去参加读书分享会,请用树状图法或列表法求所选2名同学中有男生的概率22. 阅读材料,解答问题:材料1
为了解方程 , 如果我们把看作一个整体,然后设 , 则原方程可化为 , 经过运算,原方程的解为 , . 我们把以上这种解决问题的方法通常叫做换元法.
材料2
已知实数m,n满足 , , 且 , 显然m,n是方程的两个不相等的实数根,由书达定理可知 , .
根据上述材料,解决以下问题:
(1)、直接应用:方程的解为;
(2)、间接应用:已知实数a,b满足: , 且 , 求的值;
(3)、拓展应用:已知实数m,n满足: , 且 , 求的值.
23. 某校为配合疫情防控需要,每星期组织学生进行核酸抽样检测;防疫部门为了解学生错峰进入操场进行核酸检测情况,调查了某天上午学生进入操场的累计人数y(单位:人)与时间x(单位:分钟)的变化情况,发现其变化规律符合函数关系式:数据如下表.时间x(分钟)
0
1
2
3
…
8
累计人数y(人)
0
150
280
390
…
640
640
(1)、求a,b,c的值;(2)、如果学生一进入操场就开始排队进行核酸检测,检测点有4个,每个检测点每分钟检测5人,求排队人数的最大值(排队人数-累计人数-已检测人数);(3)、在(2)的条件下,全部学生都完成核酸检测需要多少时间?如果要在不超过20分钟让全部学生完成核酸检测,从一开始就应该至少增加几个检测点?