浙江省诸暨市浣江教育共同体2021-2022学年八年级上学期期中考试数学试题
试卷更新日期:2022-09-14 类型:期中考试
一、单选题
-
1. 下列图形:
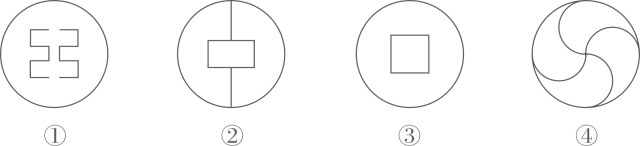
其中是轴对称图形且有两条对称轴的是( )
A、①② B、②③ C、②④ D、③④2. 一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是( ) A、x>1 B、x≥1 C、x>3 D、x≥33. 如图,已知 , 增加下列条件,不能肯定的是( )
A、x>1 B、x≥1 C、x>3 D、x≥33. 如图,已知 , 增加下列条件,不能肯定的是( ) A、 B、 C、 D、4. 如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=3,ED=6,则EB+DC的值为( )
A、 B、 C、 D、4. 如图,在△ABC中,ED∥BC,∠ABC和∠ACB的平分线分别交ED于点G、F,若FG=3,ED=6,则EB+DC的值为( ) A、7 B、8 C、9 D、105. 一副三角板,按如图所示叠放在一起,则图中∠a的度数是( )
A、7 B、8 C、9 D、105. 一副三角板,按如图所示叠放在一起,则图中∠a的度数是( )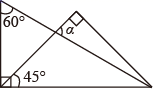 A、105° B、75° C、110° D、120°6. 已知等腰三角形一腰上的高线等于另一腰长的一半,那么这个等腰三角形的一个底角等于( )A、15°或75° B、15° C、75° D、15°或30°7. 关于 的不等式组 只有3个整数解,求 的取值范围( )A、 B、 C、 D、8. 如图,Rt△ABC中,∠C=90°,∠A<∠B , 且∠A≠30°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点P在△ABC的其他边上,则可以画出不同的点P的个数为( )
A、105° B、75° C、110° D、120°6. 已知等腰三角形一腰上的高线等于另一腰长的一半,那么这个等腰三角形的一个底角等于( )A、15°或75° B、15° C、75° D、15°或30°7. 关于 的不等式组 只有3个整数解,求 的取值范围( )A、 B、 C、 D、8. 如图,Rt△ABC中,∠C=90°,∠A<∠B , 且∠A≠30°,以△ABC的一边为边画等腰三角形,使得它的第三个顶点P在△ABC的其他边上,则可以画出不同的点P的个数为( )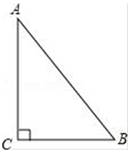 A、4 B、5 C、6 D、79. 如图, ,点B和点C是对应顶点, ,记 ,当 时, 与 之间的数量关系为( )
A、4 B、5 C、6 D、79. 如图, ,点B和点C是对应顶点, ,记 ,当 时, 与 之间的数量关系为( ) A、 B、 C、 D、10. 如图,△ABC中,AD垂直BC于点D , 且AD=BC , BC上方有一动点P满足 ,则点P到B、C两点距离之和最小时,∠PBC的度数为( )
A、 B、 C、 D、10. 如图,△ABC中,AD垂直BC于点D , 且AD=BC , BC上方有一动点P满足 ,则点P到B、C两点距离之和最小时,∠PBC的度数为( ) A、30° B、45° C、60° D、90°
A、30° B、45° C、60° D、90°二、填空题
-
11. 若 ,那么 (填“>”“<”或“=”).12. 命题“等腰三角形两腰上的高线相等”的逆命题是命题 填“真”或“假”13. 已知等腰三角形其中一个内角为70°,则这个等腰三角形的顶角度数为.14. 如图,在△ABC中,BC边上的垂直平分线交AC于点D;已知AB=3,AC=7,BC=8,则△ABD的周长为 .
 15. 某种商品的进价为800元,标价为1200元.由于商品积压,商家准备打折销售,但要保证利润不低于20%,则至少可以打折.16. 如图,三边的中线AD、BE、CF的公共点为G, , 则图中阴影部分的面积是 .
15. 某种商品的进价为800元,标价为1200元.由于商品积压,商家准备打折销售,但要保证利润不低于20%,则至少可以打折.16. 如图,三边的中线AD、BE、CF的公共点为G, , 则图中阴影部分的面积是 . 17. 如图,在△ABC中,∠BAC为钝角,AF、CE都是这个三角形的高,P为AC的中点,若∠B=40°,则∠EPF= .
17. 如图,在△ABC中,∠BAC为钝角,AF、CE都是这个三角形的高,P为AC的中点,若∠B=40°,则∠EPF= . 18. 已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交直线AB于点D,连接CD.若∠ABC=40°,∠ACD=20°,则∠BAC的度数为 .19. 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图所示,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1 , S2 , S3 , 若正方形EFGH的边长为4,则S1+S2+S3的值为
18. 已知△ABC,按以下步骤作图:①分别以B,C为圆心,以大于BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交直线AB于点D,连接CD.若∠ABC=40°,∠ACD=20°,则∠BAC的度数为 .19. 我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图所示,它是由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1 , S2 , S3 , 若正方形EFGH的边长为4,则S1+S2+S3的值为 20. 问题背景:如图1,点C为线段AB外一动点,且AB=AC=2,若BC=CD,∠BCD=60°,连接AD,求AD的最大值.
20. 问题背景:如图1,点C为线段AB外一动点,且AB=AC=2,若BC=CD,∠BCD=60°,连接AD,求AD的最大值.解决方法:以AC为边作等边△ACE,连接BE,推出BE=AD,当点E在BA的延长线上时,线段AD取得最大值4
问题解决:如图2,点C为线段AB外一动点,且AB=AC=2,若BC=CD,∠BCD=90°,连接AD,当AD取得最大值时,∠ACD的度数为 .

三、解答题
-
21. 解不等式组: ,并把解集在数轴上表示出来.22. 如图,等边三角形ABC和等边三角形APQ,点P在△ABC内,点Q在△ABC外,求证:△ABP≌△ACQ.
 23. 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积.
23. 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.作AD⊥BC于D,设BD=x,用含x的代数式表示CD→根据勾股定理,利用AD作为“桥梁”,建立方程模型求出x→利用勾股定理求出AD的长,再计算三角形的面积. 24. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“奇妙三角形”.
24. 如果三角形有一边上的中线恰好等于这边的长,那么我们称这个三角形为“奇妙三角形”.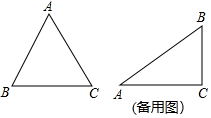 (1)、如图,在△ABC中,AB=AC= , BC=4,求证:△ABC是“奇妙三角形”;(2)、在Rt△ABC中,∠C=90°,AC= , 若△ABC是“奇妙三角形”,求BC的长.25. 某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖的纸盒.
(1)、如图,在△ABC中,AB=AC= , BC=4,求证:△ABC是“奇妙三角形”;(2)、在Rt△ABC中,∠C=90°,AC= , 若△ABC是“奇妙三角形”,求BC的长.25. 某工厂用如图甲所示的长方形和正方形纸板,做成如图乙所示的竖式与横式两种长方体形状的无盖的纸盒. (1)、现有正方形纸板162张,长方形纸板340张,若要做两种纸盒共100个,设竖式纸盒x个,需要长方形纸板张,正方形纸板张(请用含有x的式子)(2)、在(1)的条件下,有哪几种生产方案?(3)、若有正方形纸板162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<300,求a的值.26. 在Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,过点D作DE⊥AB,交BC于点E,连接AE,取AE的中点P,连接DP,CP.
(1)、现有正方形纸板162张,长方形纸板340张,若要做两种纸盒共100个,设竖式纸盒x个,需要长方形纸板张,正方形纸板张(请用含有x的式子)(2)、在(1)的条件下,有哪几种生产方案?(3)、若有正方形纸板162张,长方形纸板a张,做成上述两种纸盒,纸板恰好用完.已知290<a<300,求a的值.26. 在Rt△ABC中,∠ACB=90°,AC=BC,点D为AB边上一点,过点D作DE⊥AB,交BC于点E,连接AE,取AE的中点P,连接DP,CP.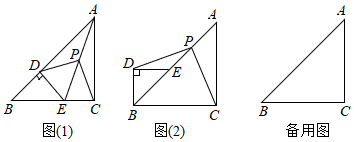 (1)、观察猜想:如图(1),DP与CP之间的数量关系是 , DP与CP之间的位置关系是.(2)、类比探究: 将图(1)中的△BDE绕点B逆时针旋转45°,(1)中的结论是否仍然成立?若成立,请就图(2)的情形给出证明;若不成立,请说明理由.(3)、问题解决: 若BC=3BD=3 , 将图(1)中的△BDE绕点B在平面内自由旋转,当BE⊥AB时,请直接写出线段CP的长.
(1)、观察猜想:如图(1),DP与CP之间的数量关系是 , DP与CP之间的位置关系是.(2)、类比探究: 将图(1)中的△BDE绕点B逆时针旋转45°,(1)中的结论是否仍然成立?若成立,请就图(2)的情形给出证明;若不成立,请说明理由.(3)、问题解决: 若BC=3BD=3 , 将图(1)中的△BDE绕点B在平面内自由旋转,当BE⊥AB时,请直接写出线段CP的长.