浙江省温州市龙湾区2021-2022学年八年级上学期期中数学试题
试卷更新日期：2022-09-14 类型：期中考试
一、单选题
-
1. 下列图形中是轴对称图形的是（ ）A、
B、
C、
D、
2. 若不等式﹣3x＜1，两边同时除以﹣3，得（ ）A、x＞﹣ B、x＜﹣ C、x＞ D、x＜3. 两边长为4和8的等腰三角形的周长为（ ）A、16 B、20 C、16或20 D、16或184. 如图，已知AD＝BC，添加下列条件还不能判定△ABC≌△BAD的是（ ）
A、AC＝BD B、∠CAB＝∠DBA C、∠ABC＝∠BAD D、△ABD的周长＝△ABC的周长5. 若m＞n，则下列不等式成立的是（ ）A、m﹣5＜n﹣5 B、 C、﹣5m＞﹣5n D、6. 可以用来说明命题“x2＜y2 ， 则x＜y”是假命题的反例是（ ）A、x＝4，y＝3 B、x＝﹣1，y＝2 C、x＝﹣2，y＝1 D、x＝2，y＝﹣37. 满足下列条件的△ABC中，不是直角三角形的是（ ）A、∠A：∠B：∠C＝3：4：5 B、∠A：∠B：∠C＝2：3：5 C、∠A+∠B＝∠C D、一个外角等于和它相邻的一个内角8. 如图，在△ABC中，AB＝AC＝9，点E在边AC上，AE的中垂线交BC于点D，若∠ADE＝∠B，CD＝3BD，则CE等于（ ）
A、3 B、2 C、 D、9. 如图所示的2×4的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形，则点A到BC的距离等于（ ）
A、 B、2 C、 D、10. 如图，OA⊥OB，OB＝4，P是射线OA上一动点，连接BP，以B为直角顶点向上作等腰直角三角形，在OA上取一点D，使∠CDO＝45°，当P在射线OA上自O向A运动时，PD的长度的变化（ ）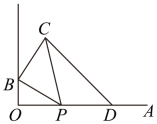
A、一直增大 B、一直减小 C、先增大后减小 D、保持不变二、填空题
-
11. “等腰三角形的两个底角相等．”请写出它的逆命题： ．12. 边长为1的等边三角形的面积是 ．13. 等腰三角形的一个底角为35°，则顶角的度数是度．14. 如图，△ABC是等边三角形，点D为AC边上一点，以BD为边作等边△BDE，连接CE．若BC＝4，CD＝1，则CE＝ ．
15. 已知不等式（a﹣1）x＞a﹣1的解集是x＜1，则a的取值范围为 ．16. 如图，在等腰△OAB中，OA＝OB＝2，∠OAB＝90°，以AB为边向右侧作等腰Rt△ABC，则OC的长为 ．
17. 如图，点B为线段AQ上的动点，AQ＝8 ，以AB为边作正△ABC，以BC为底边作等腰三角形PCB，则PQ的最小值为 .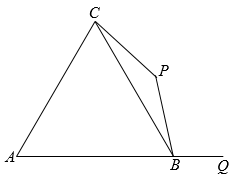
18. 如图，在△ABC中，∠ACB＝90°，以AC，BC和AB为边向上作正方形ACED和正方形BCMI和正方形ABGF，点G落在MI上，若AC+BC＝7，空白部分面积为16，则图中阴影部分的面积是 ．
三、解答题
-
19. 解不等式：(1)、2（x﹣1）﹣3（3x+2）＞x+5．(2)、 ．20. 已知：如图，AB∥DE，AC∥DF，AB＝DE．求证：BE＝CF．
21. 如图，在所给的6×6方格中，点A，B，P都在小方格的格点上，按下列要求画图，所画的点都必须落在方格纸的格点上．
(1)、请画出两个等腰直角三角形ABC，使点P在△ABC内部（分别在图1、2中画出示意图，不能重复）．(2)、请画一个等腰三角形ABC，使点P落在△ABC的对称轴上（在图3中画出示意图）．22. 在《几何原本》著作中，命题47：在直角三角形中，直角所对的边上的正方形等于夹直角两边上的正方形的和．古代人还没有发明勾股定理，他们如何证明这个命题是真命题．已知△ABC，∠BAC＝90°；求证：以BC为边正方形的面积＝以BA为边正方形的面积+以AC为边正方形的面积．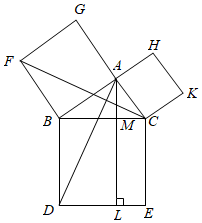
23. 如图，∠ACB＝90°，CD⊥AB于点D，AF平分∠CAB交CD于点E，交BC于点F，作EG∥AB交CB于点G．
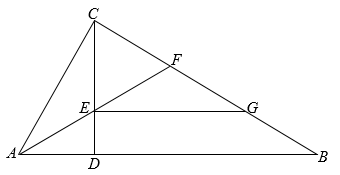(1)、求证：△CEF是等腰三角形；(2)、求证：CF＝BG；(3)、若F是CG的中点，EF＝1，求AB的长．24. 如图：已知△BCD是等腰直角三角形，且∠DCB＝90°，过点D作AD∥BC，使AD＝BC，在AD上取一点E，连结CE，点B关于CE的对称点为B1 ， 连结B1D，并延长B1D交BA的延长线于点F，延长CE交B1F于点G，连结BG．
(1)、求证：∠CBG＝∠CDB1；(2)、若AE＝DE，BC＝10，求BG长；(3)、在（2）的条件下，H为直线BG上一点，使△HCG为等腰三角形，则所有满足要求的BH的长是 _ ． （直接写出答案）