浙江省衢州市教学联盟体2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图案中，轴对称图形是（　　）

A、 B、 C、 D、

查看试题解析
2. 已知，在直角△ABC中，∠C为直角，∠B是∠A的2倍，则∠A的度数是（）

A、 $30 °$ B、 $50 °$ C、 $70 °$ D、 $90 °$

查看试题解析
3. 下列长度的三条线段（单位：cm）能组成三角形的是（）

A、1，2，1 B、4，5，9 C、6，8，13 D、2，2，4

查看试题解析
4. 为说明命题“若 $a > b$ ，则 $a^{2} > b^{2}$ ”是假命题，所列举反例正确的是（）

A、 $a = 5 ， b = 3$ B、 $a = - 1 ， b = - 2$ C、 $a = 2 ， b = 1$ D、 $a = - \frac{1}{2} ， b = - \frac{1}{3}$

查看试题解析
5. 下列各命题的逆命题成立的是（）

A、全等三角形的对应角相等 B、如果两个数相等，那么它们的绝对值相等 C、两直线平行，同位角相等 D、如果两个角都是45°，那么这两个角相等

查看试题解析
6. 以下四种作 $△ A B C$ 边AC上的高，其中正确的作法是（）

A、 B、 C、 D、

查看试题解析
7. 等腰三角形其中两条边的长度为5和11，则该等腰三角形的周长为（）

A、21 B、27 C、21或32 D、21或27

查看试题解析
8. 如图，以Rt△ABC的三边为边长向外作正方形，三个正方形的面积分别为 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ ，若 $S_{1} = 13$ ， $S_{2} = 12$ ，则 $S_{3}$ 的值为（）

A、1 B、5 C、25 D、144

查看试题解析
9. 如图，关于△ABC ，给出下列四组条件：
①△ABC中，AB＝AC；

②△ABC中，∠B＝56°，∠BAC＝68°；

③△ABC中，AD⊥BC ， AD平分∠BAC；

④△ABC中，AD⊥BC ， AD平分边BC ．

其中，能判定△ABC是等腰三角形的条件共有（　　）

A、1组 B、2组 C、3组 D、4组

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A D$ 是高， $B E$ 是中线， $C F$ 是角平分线， $C F$ 交 $A D$ 于点 $G$ ，交 $B E$ 于点 $H$ ，下面四个说法中，其中正确的是（）
① $△ A B E$ 的面积等于 $△ B C E$ 的面积；② $∠ A F G = ∠ A G F$ ；③ $∠ F A G = 2 ∠ A C F$ ；④ $B H = C H$

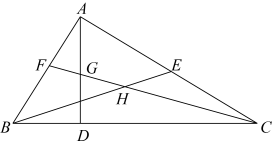A、①②③④ B、①②③ C、②④ D、①③

查看试题解析

二、填空题

11. “x的2倍与3的差是大于零”用不等式表示为．

查看试题解析
12. 已知三角形的三边长分别是4、5、x，则x的取值范围是．

查看试题解析
13. 如图所示，在Rt△ABC中，CD是斜边AB上的高，∠ACD=40°，则∠EBC=度．

查看试题解析
14. 直角三角形的两边长分别为6和8，则该直角三角形斜边上的中线为.

查看试题解析
15. 如图，在△ABC中，点D，E，F分别是BC，AD，EC的中点，若△ABC的面积等于36，则△BEF的面积为．

查看试题解析
16. 如图，在 $Δ A B C$ 中， $A B = 6 ， A C = \sqrt{3} ， ∠ A = 30 °$ ，作 $Δ A B C$ 关于直线 $l$ 的轴对称图形 $Δ E B D ，$ 点 $F$ 是 $B E$ 的中点，若点 $A ， C ， F$ 在同一直线上，则 $C D$ 的长为.

查看试题解析

三、解答题

17. 如图， $B C / / E F$ ， $A D = B E$ ， $B C = E F$ ，试说明 $△ A B C ≌ △ D E F$ ．
解： $∵ A D = B E$
∴      ▲      ＋ $D B = B E + D B$ ；即      ▲       $= D E$ ．
$∵ B C / / E F$
$∴ ∠ A B C = ∠ E$ （    ），
在 $△ A B C$ 和 $△ D E F$ 中
${\begin{array}{l} B C = E F (已知) \\ ∠ A B C = ∠ E \\ ________=________ \end{array}$
$∴ △ A B C ≌ △ D E F$ （    ）

查看试题解析
18. 如图，AB＝AC，BD＝DC，DF⊥AB，DE⊥AC，垂足分别是F，E．求证：DE＝DF．

查看试题解析
19. 尺规作图．如图，在Rt△ABC中， $∠ C = 90 °$ ．

(1)、求作线段AB的中垂线；

(2)、求作∠BAC的角平分线．

查看试题解析
20. 如图，在△ABC和△DCB中，BA⊥CA于A，CD⊥BD于D，AC＝BD，AC与BD相交于点O.

(1)、求证：△ABC≌△DCB；

(2)、若∠OBC＝30°，求∠AOB的大小.

查看试题解析
21. 如图，在Rt△ABC中， $∠ A B C = 90 ° ， A B = 3 ， A C = 5$ ，点E在BC上，将△ABC沿AE折叠，使点B落在AC边上的点 $B^{'}$ 处，求BE的长．

查看试题解析
22. 如图，已知△ABF≌△CDE.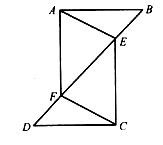

(1)、若∠B＝30°，∠DCF＝40°，求∠EFC的度数；

(2)、若BD=10，EF=2，求BF的长.

查看试题解析
23. 如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动(D不与B、C重合)，连接AD，作∠ADE=40°，DE与AC交于E。

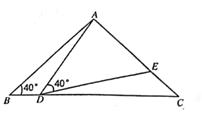(1)、当∠BDA=115°时，∠BAD=°，∠DEC=°，当点D从B向C运动时，∠BDA逐渐变(填“大”或“小”)；

(2)、当DC等于多少时，△ABD与△DCE全等?请说明理由；

(3)、在点D的运动过程中，△ADE的形状可以是等腰三角形吗?若可以，请直接写出∠BDA的度数；若不可以，请说明理由。

查看试题解析
24. 如图

(1)、如图1， $△ A B C$ 中，作 $∠ A B C$ 、 $∠ A C B$ 的角平分线相交于点O，过点O作 $E F / / B C$ 分别交 $A B$ 、 $A C$ 于E、F．
①求证： $O E = B E$ ；
②若 $△ A B C$ 的周长是25， $B C = 9$ ，试求出 $△ A E F$ 的周长；

(2)、如图2，若 $∠ A B C$ 的平分线与 $∠ A C B$ 外角 $∠ A C D$ 的平分线相交于点P，连接 $A P$ ，试探求 $∠ B A C$ 与 $∠ P A C$ 的数量关系式．

查看试题解析