浙江省杭州市余杭区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-14 类型:期中考试
一、单选题
-
1. 以下长度的线段能和长度为2,6的线段组成三角形的是( )A、2 B、4 C、6 D、92. 下列图形不一定是轴对称图形的是( )A、直角三角形 B、等腰三角形 C、线段 D、圆3. 如图,在中, , , 则外角的度数是( )
 A、35° B、45° C、80° D、100°4. 如图,已知△ABC≌△DAE,BC=2,DE=5,则CE的长为( )
A、35° B、45° C、80° D、100°4. 如图,已知△ABC≌△DAE,BC=2,DE=5,则CE的长为( )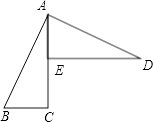 A、2 B、2.5 C、3 D、3.55. 三角形的三边长分别为a、b、c,且满足 , 则这个三角形是( )A、等边三角形 B、钝角三角形 C、直角三角形 D、锐角三角形6. 在锐角中, , , 高 , 则BC的长度为( )A、16 B、15 C、14 D、137. 已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( )
A、2 B、2.5 C、3 D、3.55. 三角形的三边长分别为a、b、c,且满足 , 则这个三角形是( )A、等边三角形 B、钝角三角形 C、直角三角形 D、锐角三角形6. 在锐角中, , , 高 , 则BC的长度为( )A、16 B、15 C、14 D、137. 已知,△ABC,△DEF,△XYZ的相关数据如图所示,则( ) A、 B、 C、 D、8. 记的三边分别为a,b,c,则无法判断为直角三角形的是( )A、 B、 C、 D、9. 如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( )
A、 B、 C、 D、8. 记的三边分别为a,b,c,则无法判断为直角三角形的是( )A、 B、 C、 D、9. 如图, 中, , , 的垂直平分线分别交 于点E,F,与 , 分别交于点D,G,则 的度数为( ) A、 B、 C、 D、10. 如图,已知每个小方格的边长为1,A、B、C三点都在小方格的顶点上,则点C到AB所在直线的距离等于( )
A、 B、 C、 D、10. 如图,已知每个小方格的边长为1,A、B、C三点都在小方格的顶点上,则点C到AB所在直线的距离等于( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 在中, , , 则 .12. 如图是单位长度为1的正方形网格,则°.
 13. 到的三边距离相等的点是的;到的三个顶点距离相等的点是的 . (填写序号即可:①三条中线的交点;②三条内角平分线的交点;③三条高线的交点;④三条边的垂直平分线的交点)14. 如图,在 中, ,AD平分 .若 , ,则点D到AB的距离为 .
13. 到的三边距离相等的点是的;到的三个顶点距离相等的点是的 . (填写序号即可:①三条中线的交点;②三条内角平分线的交点;③三条高线的交点;④三条边的垂直平分线的交点)14. 如图,在 中, ,AD平分 .若 , ,则点D到AB的距离为 . 15. 在Rt中, , CD是斜边AB上的中线,已知 , , 则的周长等于 .16. 若等腰三角形的底边长为6,则它的腰长x的取值范围是;若等腰三角形的腰长为6,则它的底边长y的取值范围是 .
15. 在Rt中, , CD是斜边AB上的中线,已知 , , 则的周长等于 .16. 若等腰三角形的底边长为6,则它的腰长x的取值范围是;若等腰三角形的腰长为6,则它的底边长y的取值范围是 .三、解答题
-
17. 已知 , 按要求完成下列画图.(不写作法,保留作图痕迹并写出结论)
 (1)、用尺规作AC边上的中线.(2)、用尺规作角平分线AM.18. 已知等腰三角形一腰上的中线把这个三角形的周长分成15和16两部分,求这个等腰三角形的腰长和底边的长.19. 如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,已知∠DCB=2∠B,求∠ACD的度数.
(1)、用尺规作AC边上的中线.(2)、用尺规作角平分线AM.18. 已知等腰三角形一腰上的中线把这个三角形的周长分成15和16两部分,求这个等腰三角形的腰长和底边的长.19. 如图,在△ABC中,∠A=90°,∠ACB的平分线交AB于D,已知∠DCB=2∠B,求∠ACD的度数.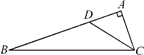 20. 如图,在等边△ABC中,点 , 分别在边 , 上, , 过点作 , 交的延长线于点 , 若 , 求的长.
20. 如图,在等边△ABC中,点 , 分别在边 , 上, , 过点作 , 交的延长线于点 , 若 , 求的长.


