湖北省潜江市2021-2022学年七年级上学期10月联考数学试题

试卷更新日期：2022-09-14 类型：月考试卷

进入出卷网下载

一、单选题

1. 如果向北走3km记作+3km，那么-2km表示（）

A、向东走2km B、向南走2km C、向西走2km D、向北走2km

查看试题解析
2. -2的绝对值是（）

A、2 B、 $\frac{1}{2}$ C、 $- \frac{1}{2}$ D、 $- 2$

查看试题解析
3. 地球距太阳约有150 000 000千米，用科学记数法表示为（）

A、0.15×10⁹千米 B、1.5×10⁸千米 C、15×10⁷千米 D、1.5×10⁹千米

查看试题解析
4. 用四舍五入法对0.05046分别取近似值，其中错误的是（）．

A、0.1（精确到0.1） B、0.05（精确到千分位） C、0.05（精确到百分位） D、0.050（精确到千分位）

查看试题解析
5. 下列各对数中，互为相反数的是（）

A、－(＋3)与＋(－3) B、－(－4)与|－4| C、－3²与(－3)² D、－2³与(－2)³

查看试题解析
6. 如图是一个计算程序，若输入a的值为﹣1，则输出的结果应为（）

A、7 B、﹣5 C、1 D、5

查看试题解析
7. 下列说法正确的是（）

A、一个数，如果不是正数，必定是负数 B、有理数的绝对值一定是正数 C、两个有理数相加，和一定大于每个加数 D、相反数等于本身的数是0

查看试题解析
8. 如图，a，b表示两个有理数，则（）

A、 $- a - b > 0$ B、a＋b＞0 C、 $- \frac{1}{a} > \frac{1}{b}$ D、 $a + 2 b > 0$

查看试题解析
9. 在数–6，3，5，–2中任取两个数相乘，所得积最小的是（）

A、-18 B、-30 C、-10 D、-6

查看试题解析
10. 若“!”是一种数学运算符号，并且1!＝1，2!＝2×1，3!＝3×2×1，4!＝4×3×2×1，……，则 $\frac{100!}{98!}$ 的值是为（）

A、 $\frac{50}{40}$ B、99! C、9900 D、2!

查看试题解析

二、填空题

11. － $\frac{2}{3}$ 的倒数是；－ $\frac{2}{3}$ 的平方是.3的相反数是．

查看试题解析
12. 一天小明和冬冬利用温差来测量山峰的高度．冬冬在山脚测得的温度是25℃，小明此时在山顶测得的温度是16℃，已知该地区高度每升高100米，气温下降0.6℃，问这个山峰的高度是米．

查看试题解析
13. 如果数轴上的点A对应有理数为-3，那么与A点相距5个单位长度的点所对应的有理数为．

查看试题解析
14. 已知a ， b互为相反数，c ， d互为倒数，m是绝对值最小的数，则 $3 a + 2 b + b c d + \frac{m}{4 c d}$ 的值为

查看试题解析
15. 3.05×10⁶精确到位

查看试题解析
16. 若 $0 < m < 1$ ， $m$ 、 $m^{2}$ 、 $\frac{1}{m}$ 的大小关系是．

查看试题解析
17. 若｜2x－4｜与｜y－3｜互为相反数，则2x－y＝.

查看试题解析
18. 若 $a + b + c < 0 ， a b c > 0$ ，则 $\frac{a}{| a |} + \frac{2 a b}{| a b |} + \frac{3 a b c}{| a b c |}$ 的值为．

查看试题解析
19. 李明与王伟在玩一种计算的游戏，计算的规则是 $| \begin{matrix} a & b \\ c & d \end{matrix} |$ =ad﹣bc，李明轮到计算 $| \begin{matrix} 3 & 2 \\ 5 & 1 \end{matrix} |$ ，根据规则 $| \begin{matrix} 3 & 2 \\ 5 & 1 \end{matrix} |$ =3×1﹣2×5=3﹣10=﹣7，现在轮到王伟计算 $| \begin{matrix} 2 & 3 \\ 6 & 5 \end{matrix} |$ ，请你帮忙算一算，得.

查看试题解析
20. 正整数按下图的规律排列.请写出第20行，第21列的数字.

查看试题解析

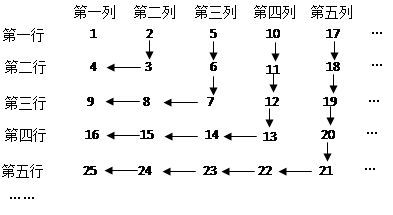
三、解答题

21. 计算：

(1)、4.7－（－8.9）－7.4＋（－6）

(2)、 2×（－5）+（－56）÷（6－10）

(3)、 $25 \times \frac{3}{4} - (- 25) \times \frac{1}{2} + 25 \times (- \frac{1}{4})$

(4)、 $- 1^{2} + (- 6) \div (- \frac{1}{3}) - 3 \times (- 2)^{2}$

查看试题解析
22. 把下列各数填在相应的括号里：
﹣8，0.275， $\frac{22}{7}$ ，0，﹣1.04，﹣（﹣3），﹣ $\frac{1}{3}$ ，|﹣2|

正数集合{        …}

负整数集合{      …}

分数集合{        …}

负数集合{        …}.

查看试题解析
23. 在数轴上表示下列各数，并用“<” 排列各数：
–3， 1， $| - 2 \frac{1}{2} |$ ，－1.5，－（－2）．

查看试题解析
24. 阅读下列材料：
计算： $\frac{1}{24} \div (\frac{1}{3} - \frac{1}{4} + \frac{1}{12})$
解法一：原式= $\frac{1}{24} \div \frac{1}{3} - \frac{1}{24} \div \frac{1}{4} + \frac{1}{24} \div \frac{1}{12} = \frac{1}{24} \times 3 - \frac{1}{24} \times 4 + \frac{1}{24} \times 12 = \frac{11}{24}$
解法二：原式= $\frac{1}{24} \div (\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) = \frac{1}{24} \div \frac{2}{12} = \frac{1}{24} \times 6 = \frac{1}{4}$
解法三：原式的倒数= $(\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) \div \frac{1}{24} = (\frac{1}{3} - \frac{1}{4} + \frac{1}{12}) \times 24 = \frac{1}{3} \times 24 - \frac{1}{4} \times 24 + \frac{1}{12} \times 24 = 4$
所以，原式= $\frac{1}{4}$ ．

(1)、上述得到的结果不同，你认为解法是错误的；

(2)、请你选择合适的解法计算： $(- \frac{1}{42}) \div (\frac{1}{6} - \frac{3}{14} - \frac{2}{3} + \frac{2}{7})$

查看试题解析
25. 已知 $| x | = 4$ ， $| y | = 5$ ，且 $x > y$ ，求 $x + y$ 的值．

查看试题解析
26. 某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位：km）：

第1批

第2批

第3批

第4批

第5批

5km

2km

﹣4km

﹣3km

10km

(1)、接送完第5批客人后，该驾驶员在公司的什么方向，距离公司多少千米？

(2)、若该出租车每千米耗油0.1升，那么在这过程中共耗油多少升？

(3)、若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？

查看试题解析
27. 已知数轴上A、B两点表示的数分别为a，b，且a，b满足|a+20|+（b-13）²=0，点C表示的数为16，点D表示的数为-7．

(1)、A，C两点之间的距离为；

(2)、已知|m－n|可理解为数轴上表示数m、n的两点之间的距离．
若点P在数轴上表示的数为x，则满足|x+2|+|x-3|=5的所有的整数x的和为；满足|x+2|+|x-3|=9的x值为．

(3)、点A，B从起始位置同时出发相向匀速运动，点A的速度为6个单位长度/秒，点B的速度为2个单位长度/秒，当点A运动到点C时，迅速以原来的速度返回，到达出发点后，又折返向点C运动，点B运动至点D后停止运动，当点B停止运动时，点A也停止运动，求在此运动过程中，求A，B两点同时到达的点在数轴上表示的数．

查看试题解析

第1批	第2批	第3批	第4批	第5批
5km	2km	﹣4km	﹣3km	10km