2022年苏科版初中数学七年级上册3.4 合并同类项同步练习

试卷更新日期：2022-09-14 类型：同步测试

进入出卷网下载

一、夯实基础

1. 下列各组单项式中，是同类项的是（）

A、5a，3a B、-2x²y，3xy C、4x² ， 3x D、3ab，- 5ab²

查看试题解析
2. 下列计算正确的是（）

A、 $3 x^{2} + 2 x^{2} = 5 x^{4}$ B、 $3 a + 2 b = 6 a b$ C、 $a^{3} + a^{2} = a^{5}$ D、 $x^{2} - 3 x^{2} = - 2 x^{2}$

查看试题解析
3. 若 $- 2 a^{m} b^{4}$ 与 $5 a^{2} b^{m - 2 n}$ 是同类项，则 $m - n$ 的值是（）

A、3 B、 $- 3$ C、1 D、 $- 1$

查看试题解析
4. 已知- $5 x^{a} y^{3}$ 与 $2 x^{2} y^{b}$ 为同类项，则 $a^{b}$ 的值为（）

A、2 B、4 C、6 D、8

查看试题解析
5. 有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图所示，则 $| a + b | - | b - c |$ 的值为（）

A、 $a - 2 b - c$ B、 $a + c$ C、 $- a - 2 b + c$ D、 $- a - c$

查看试题解析
6. 计算－x² ＋ 2x²的结果是.

查看试题解析
7. 如果 $3 x^{2 n} y^{3}$ 与 $- 2 x^{4} y^{m + 1}$ 是同类项，则 $m - n =$ .

查看试题解析
8. 若单项式 $\frac{5}{7} a x^{2} y^{n + 1}$ 与 $- \frac{7}{5} a x^{m} y^{4}$ 的差仍是单项式，则 $m - 2 n =$ ．

查看试题解析
9. 判断下列各题中的两个项是不是同类项：

(1)、 $- 2 a^{2} b^{3}$ 与 $3 b^{3} a^{2}$ ；

(2)、 $- \frac{1}{5} x^{2} y z$ 与 $- \frac{1}{5} x y^{2} z$ ；

(3)、7与x；

(4)、﹣3与0．

查看试题解析
10. 化简：

(1)、2ax²﹣3ax²﹣7ax²；

(2)、（x﹣1）﹣（2x+1）．

查看试题解析
11. 把(x－y)看成一个整体合并同类项：5(x－y)²＋2(x－y)－3(x－y)²＋ $\frac{1}{2}$ (x－y)－3.5.

查看试题解析
12. 已知单项式 $- 2 x^{2 m} y^{7}$ 与单项式 $- 5 x^{6} y^{n + 8}$ 是同类项，求 $- m^{2} - n^{2021}$ 的值.

查看试题解析
13. 有理数a、b、c在数轴上的位置如图：

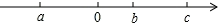(1)、判断正负，用“＞”或“＜”填空：b﹣c 0，b﹣a 0，c﹣a 0．

(2)、化简：|b﹣c|+|b﹣a|﹣|c﹣a|．

查看试题解析

二、能力提优

14. 若单项式 $- x^{m} y^{n}$ 与 $2 x^{3} y^{4}$ 是同类项，则m，n分别是（）.

A、 $m = 3$ ， $n = 4$ B、 $m = 4$ ， $n = 3$ C、 $m = - 3$ ， $n = - 4$ D、 $m = - 4$ ， $n = - 3$

查看试题解析
15. 若ax^my³+2x⁴y³＝0，则am的值为（）

A、﹣8 B、8 C、﹣6 D、6

查看试题解析
16. 已知单项式﹣x^|^a^+1|y³与2y^bx³是同类项，则a，b的值为（　　）

A、a＝2，b＝3 B、a＝﹣4，b＝3 C、a＝±2，b＝3 D、a＝2，b＝3或a＝﹣4，b＝3

查看试题解析
17. 化简：3（a﹣b）+2（a﹣b）﹣6（b﹣a）＝（）

A、b﹣a B、11a﹣11b C、2a﹣2b D、6a﹣6b

查看试题解析
18. 已知﹣17x^4my²+23x⁷yⁿ＝6x⁷y² ，则m﹣n的值是．

查看试题解析
19. 如果单项式 $\frac{1}{2} x^{a + b} y^{3}$ 与 $5 x^{2} y^{b}$ 的和仍是单项式，则 $a - b$ 的值为.

查看试题解析
20. 已知m，n为正整数，若 $a^{2} b + 3 a - 4 a^{m - 1} b^{n}$ 合并同类项后只有两项，则 $m =$ ， $n =$ ．

查看试题解析
21. 若有理数a、b、c在数轴上的位置如图所示，则 $| a - b | - | b + c |$ 可化简为.

查看试题解析
22.

(1)、若单项式 $- 2 a^{2 m - 1} b^{2}$ 与 $a b^{n - 3}$ 的和仍是单项式，求m，n的值；

(2)、若多项式 $3 x^{n - 1} - x^{n} + 2 x^{m - 1}$ 可化为六次二项式，求 $2 n^{2} - 3 m + 1$ 的值.

查看试题解析
23. 已知－x^m^－2ny^m^＋n与－3x⁵y⁶的和是单项式，求 ${(m - 2 n)}^{2}$ －5 $(m + n)$ －2 ${(m - 2 n)}^{2}$ ＋(m＋n)的值．

查看试题解析
24. 若关于x，y的多项式my³＋3nx²y＋2y³－x²y＋y不含三次项，求2m＋3n的值．

查看试题解析
25. 已知代数式2x²+ax﹣y+6﹣2bx²+3x﹣5y﹣1的值与字母x的取值无关，求 $\frac{1}{3}$ a³﹣2b²﹣ $\frac{1}{4}$ a³+3b²的值．

查看试题解析
26. 已知有理数 $a 、 b 、 c$ 在数轴上的对应点如图，化简 $| a - b | - | a + b | + | a | + | a - c |$ ．

查看试题解析
27. 阅读材料：我们知道， $4 x - 2 x + x = (4 - 2 + 1) x = 3 x$ ，类似地，我们把 $(a + b)$ 看成一个整体，则 $4 (a + b) - 2 (a + b) + (a + b) = (4 - 2 + 1) (a + b) = 3 (a + b)$ .“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛.尝试应用整体思想解决下列问题：

(1)、把 ${(a - b)}^{2}$ 看成一个整体，合并 $3 {(a - b)}^{2} - 6 {(a - b)}^{2} + 2 {(a - b)}^{2}$ ；

(2)、已知 $a - 2 b = 3$ ， $2 b - c = - 5$ ， $c - d = 10$ ，求 $(a - c) + (2 b - d) - (2 b - c)$ 的值.

查看试题解析

三、延伸拓展

28. M＝x^my³ ， N＝﹣x²y³+2xy³ ， Q＝﹣xⁿy³都是关于x，y的整式，若M+N的结果为单项式，N+Q的结果为五次多项式，则常数m，n之间的关系是（）

A、m＝n+1 B、m＝n C、m＝n+1或m＝n D、m＝n或m＝n﹣1

查看试题解析
29. 已知 $a < - 1$ ， $- 1 \leq c \leq 0$ ， $a < b < c$ ，则 $| a + b + c | - | b - c | - | a - c - 1 |$ 的最小值为，最大值为.

查看试题解析
30. 阅读材料：我们知道，4x﹣2x+x=（4﹣2+1）x=3x，类似地，我们把（a+b）看成一个整体，则4（a+b）﹣2（a+b）+（a+b）=（4﹣2+1）（a+b）=3（a+b）.“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛.尝试应用整体思想解决下列问题：

(1)、把 ${(a - b)}^{2}$ 看成一个整体，合并 $3 {(a - b)}^{2} - 6 {(a - b)}^{2} + 2 {(a - b)}^{2}$ .

(2)、已知 $x^{2} - 2 y = 4$ ，求 $3 x^{2} - 6 y - 21$ 的值；

(3)、已知a﹣2b=3，2b﹣c=﹣5，c﹣d=10，求（a﹣c）+（2b﹣d）﹣（2b﹣c）的值.

查看试题解析

2022年苏科版初中数学七年级上册3.4 合并同类项 同步练习

一、夯实基础

二、能力提优

三、延伸拓展

2022年苏科版初中数学七年级上册3.4 合并同类项同步练习