贵州省六盘水市2021-2022学年七年级上学期第一次月考数学试题
试卷更新日期:2022-09-14 类型:月考试卷
一、单选题
-
1. 若﹣a>|﹣5|,则a的值可以是( )A、﹣6 B、﹣3 C、4 D、62. 下列计算正确的是( ).A、 B、 C、 D、3. |﹣2021|等于( )A、﹣2021 B、2021 C、 D、﹣4. 有一种记分方法:以160分记为+10分,某同学得143分,则应记为( )A、+7分 B、﹣7分 C、+3分 D、﹣3分5. 将算式 写成省略加号的和的形式,正确的是( )A、 B、 C、 D、6. 若M﹣1的相反数是3,那么﹣M的值是( )A、+2 B、﹣2 C、+3 D、﹣37. 在下列选项中,具有相反意义的量的是( )A、气温升高3℃与气温为﹣3℃ B、盈利与亏损 C、胜三局与负四局 D、向东行20米和向南行20米8. 如图所示的几何体,从上面看到的形状图是( )
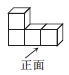 A、
A、 B、
B、 C、
C、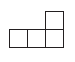 D、
D、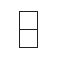 9. 下列所画数轴正确的是( )A、
9. 下列所画数轴正确的是( )A、 B、
B、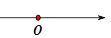 C、
C、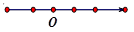 D、
D、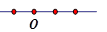 10. 如图所示的是图纸上一个零件的标注,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )
10. 如图所示的是图纸上一个零件的标注,现有下列直径尺寸的产品(单位:mm),其中不合格的是( )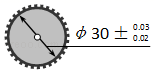 A、29.8mm B、30.03mm C、30.02mm D、29.98mm11. 有理数a, b在数轴上的对应点如图所示,则下面式子中正确的有( )个
A、29.8mm B、30.03mm C、30.02mm D、29.98mm11. 有理数a, b在数轴上的对应点如图所示,则下面式子中正确的有( )个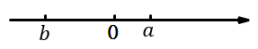
(1)b<0<a;(2)︱a︱<︱b︱;(3)ab>0;(4)a-b>a+bA、1个 B、2个 C、3个 D、4个12. 按如下的方法构造一个多位数:先任意写一个整数n(0<n<10)作为第一位上的数字,将这个整数n乘以3,若积为一位数,则将其作为第2位上的数字,若积为两位数,则将其个位数字作为第2位上的数字;再将第2位上的数字乘以3,若积为一位数,则将其作为第3位上的数字,若积为两位数,则将其个位数字作为第3位上的数字;…以此类推.若先任意写的一个整数n是7作为第一位上的数字,进行2020次如上操作后得到了第2021位上的数字,则第2021位上的数字是( )A、1 B、3 C、7 D、9二、填空题
-
13. 比较大小:14. 已知|a|=3,|b|=5,且ab<0,则a﹣b= .15. 一架直升机从高度为500米的位置开始,先以20米/秒的速度垂直上升60秒,再以12米/秒的速度垂直下降100秒,这时飞机所在的高度是米.16. 若要使图中平面展开图折叠成正方体后,使得相对面上的数的和相等,则 .

三、解答题
-
17. 计算:(1)、19+(﹣6.9)+(﹣3.1)+(﹣8.35);(2)、﹣48×(﹣3﹣).18. 某商场一批物品每箱重量标准为5千克,质量检验员抽查其中5箱的重超过标准的记为“+”,不足的记为“﹣”,分别记为﹣0.1、﹣0.2、+0.3、+0.1、+0.5,问这5箱物品的平均重量为多少千克?19. 有理数a,b,c在数轴上的位置如图所示,试化简下式:|a﹣c|﹣|a﹣b|﹣|b﹣c|+|3a|.
 20. 将6个棱长为3cm的小正方体在地面上堆叠成如图所示的几何体,然后将需露出的表面部分染成红色.
20. 将6个棱长为3cm的小正方体在地面上堆叠成如图所示的几何体,然后将需露出的表面部分染成红色. (1)、画出分别从正面、左面、上面观察所看到这个几何体的形状图.(2)、求该几何体被染成红色部分的面积.21. 根据下面给出的数轴,解答下面的问题:
(1)、画出分别从正面、左面、上面观察所看到这个几何体的形状图.(2)、求该几何体被染成红色部分的面积.21. 根据下面给出的数轴,解答下面的问题: (1)、请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: , B:;(2)、观察数轴,与点A的距离为3的点表示的数是:;(3)、若将数轴折叠,使A点与﹣3表示的点重合,则B点与数表示的点重合;(4)、若数轴上M、N两点之间的距离为2021(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: , N: .22. 某粮仓原有大米152吨,某一周该粮仓大米的进出情况如表:(运进大米记作“+”,运出大米记作“﹣”,例如:当天运进大米8吨,记作+8吨;当天运出大米15吨,记作﹣15吨)
(1)、请你根据图中A、B两点的位置,分别写出它们所表示的有理数A: , B:;(2)、观察数轴,与点A的距离为3的点表示的数是:;(3)、若将数轴折叠,使A点与﹣3表示的点重合,则B点与数表示的点重合;(4)、若数轴上M、N两点之间的距离为2021(M在N的左侧),且M、N两点经过(3)中折叠后互相重合,则M、N两点表示的数分别是:M: , N: .22. 某粮仓原有大米152吨,某一周该粮仓大米的进出情况如表:(运进大米记作“+”,运出大米记作“﹣”,例如:当天运进大米8吨,记作+8吨;当天运出大米15吨,记作﹣15吨)某粮仓大米一周进出情况表(单位:吨)
星期一
星期二
星期三
星期四
星期五
星期六
星期日
﹣32
+26
﹣23
﹣16
m
+42
﹣21
若经过这一周,该粮仓存有大米108吨.
(1)、求星期五粮仓大米的进出情况;(2)、若大米进出粮仓的装卸费用为每吨15元,求这一周该粮仓需要支付的装卸总费用.23. 将n个互不相同的整数置于一排,构成一个数组.在这n个数字前任意添加“+”或“﹣”号,可以得到一个算式.若运算结果可以为0,我们就将这个数组称为“运算平衡”数组.(1)、数组1,2,3,4是否是“运算平衡”数组?若是,请在以下数组中填上相应的符号,并完成运算;▲ 1 ▲ 2 ▲ 3 ▲ 4=0
(2)、若数组1,4,6,m是“运算平衡”数组,则m的值可以是多少?(注:至少写出4个满足条件的m的值)(3)、若某“运算平衡”数组中共含有n个整数,则这n个整数需要具备什么样的规律?24. 庐江某出租车司机,在东西方向的周瑜大道上连续接送5批客人,行驶路程记录如下表(规定向东为正,向西为负,单位:km):第1批
第2批
第3批
第4批
第5批
5km
2km
﹣4km
﹣2.5km
3.5km
(1)、接送完第5批客人后,该驾驶员在起始出发地的什么方向,距离起始出发地多少千米?(2)、若该出租车每千米耗油0.2升,那么在这过程中共耗油多少升?(3)、若该出租车的计价标准为:行驶路程不超过2.5km收费6元,超过2.5km的部分按每千米1.6元收费,在这过程中该驾驶员共收到车费多少元?25. 同学们都知道,根据绝对值的几何意义,|4﹣(﹣2)|表示4与﹣2的差的绝对值,实际上也可理解为4与﹣2两数在数轴上所对应的两点之间的距离:同理|x﹣3|也可理解为x与3两数在数轴上所对应的两点之间的距离,试探索:(1)、|4﹣(﹣2)|=;(2)、找出所有符合条件的整数x,使|x﹣4|+|x+2|=6成立,并说明理由.(3)、由以上探索猜想,对于任何有理数x,|x﹣3|+|x﹣6|是否有最小值?如果有,写出最小值;如果没有,说明理由.