云南省昭通市鲁甸县2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列国产汽车品牌标志中，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若抛物线 $y = x^{2} - k x - 2$ 经过点 $(- 1 ， 3)$ ，则k的值为（）

A、-4 B、-2 C、2 D、4

查看试题解析
3. 把方程 $x^{2} - 4 x - 7 = 0$ 化成 ${(x - m)}^{2} = n$ 的形式，下列变形确的是（）

A、 ${(x - 2)}^{2} = 3$ B、 ${(x - 2)}^{2} = 11$ C、 ${(x - 4)}^{2} = 11$ D、 ${(x + 2)}^{2} = 11$

查看试题解析
4. 关于二次函数 $y = x^{2} - 2 x - 3$ 的图象与性质中，错误的是（）

A、开口向上 B、对称轴为 $x = 1$ C、y随x的增大而增大 D、与x轴有交点

查看试题解析
5. 昭通苹果以其香甜可口闻名全国，我省某水果批发商以每千克5元的价格对外批发昭通苹果，每到秋收季节，为了减少库存，决定对苹果降价销售，经过两次降价后，批发价为每千克3.2元．设平均每次降价的百分率为x，可列方程为（）

A、 $5 (1 - 2 x) = 3.2$ B、 $5 (x - 1) = 3.2$ C、 $5 {(1 - x)}^{2} = 3.2$ D、 $3.2 {(1 + x)}^{2} = 5$

查看试题解析
6. 如图，（甲）图案通过旋转后得到（乙）图案，则其旋转中心是（　　）

A、点A B、点B C、点C D、点D

查看试题解析
7. 已知三角形的两边长为2和5，第三边满足方程 $x^{2} - 7 x + 12 = 0$ ，则三角形的周长为（）

A、10 B、11 C、10或11 D、以上都不对

查看试题解析
8. 如图，抛物线 $y = a x^{2} + b x + c$ 的对称轴为直线 $x = 1$ ，下列结论中，正确的是（）

A、 $a b c > 0$ B、 $2 a + b > 0$ C、 $4 a c > b^{2}$ D、当 $x > 1$ 时， $y > 0$

查看试题解析

二、填空题

9. 抛物线 $y = - x^{2} + 5$ 的顶点坐标是．

查看试题解析
10. 在平面直角坐标系中，点P（﹣2，﹣5）关于原点对称的点的坐标是．

查看试题解析
11. 若方程 $x^{2} + k x - 3 = 0$ 的一个根为-3，则k的值为．

查看试题解析
12. 二次函数 $y = 2 x^{2}$ 的图象经过点 $A (- 1 ， y_{1})$ 、 $B (2 ， y_{2})$ ，则 $y_{1}$ $y_{2}$ ．（填“＞”“＜”或“＝”）

查看试题解析
13. 关于x的一元二次方程 $(k - 3) x^{2} + x + 1 = 0$ 有实数根，则k的最大整数值为.

查看试题解析
14. 已知正方形ABCD中，点E在CD边上，AD＝3，DE＝2，将线段AE绕点A旋转，使点E落在直线BC上的点F处，则DF的长为．

查看试题解析

三、解答题

15. 解方程：

(1)、 $x^{2} - 8 x - 2 = 0$ ；

(2)、 $2 x^{2} - x - 3 = 0$ ．

查看试题解析
16. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $∠ A C B = 30 °$ ，将 $△ A B C$ 绕点C顺时针旋转60°得到 $△ D E C$ ，点A、B的对应点分别是D、E，点F是边AC的中点，连接DF．
求证： $△ A B C ≌ △ C F D$ ．

查看试题解析
17. 现要在一个长为40m，宽为26m的矩形花园中修建等宽的小道，剩余的地方种植花草，如图所示，要使种植花草的面积为 $864 m^{2}$ ，那么小道的宽度为多少？

查看试题解析
18. 已知二次函数 $y = a x^{2} + b x + c$ 的顶点坐标为 $A (- 1 ， 4)$ ，且过点 $B (2 ， - 5)$ ．

(1)、直接写出 $a - b + c$ 的值；

(2)、求二次函数的解析式．

查看试题解析
19. 如图，在平面直角坐标系中， $△ A B O$ 的顶点均在格点上．
⑴画出 $△ A B O$ 关于x轴对称的图形 $△ A_{1} B_{1} O$ ，并写出 $A_{1}$ 的坐标；
⑵画出 $△ A B O$ 绕点O顺时针旋转90°后得到的图形 $△ A_{2} B_{2} O$ ，并写出 $B_{2}$ 的坐标．

查看试题解析
20. 已知二次函数 $y = x^{2} - 2 m x + 2 m - 1$ ．

(1)、求证：二次函数的图象与x轴总有交点；

(2)、若二次函数的图象与x轴的一个交点为原点，求方程 $x^{2} - 2 m x + 2 m - 1 = 0$ 的解．

查看试题解析
21. 为了巩固“脱贫攻坚”的成果，云南某驻村干部指导农户进行柑橘种植和销售，已知柑橘的种植成本为4元/千克，经市场调查发现，今年国庆期间柑橘的销售量y（千克）与销售单价x（元/千克）（ $4 \leq x \leq 24$ ）成如图所示函数关系．

(1)、根据函数图象提供的信息，求y与x的函数关系式；

(2)、若国庆期间销售柑橘获取的利润W元，求出销售单价定为多少元时，获得的利润最大？最大利润是多少？

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $A C = 20 c m$ ， $B C = 15 c m$ ，现有一个动点P从点A出发，以4cm/s的速度沿AC向终点C运动，动点Q同时从点C出发，以2cm/s的速度沿CB向终点B运动，当有一点到达终点时，另一点随之停止运动．设运动时间为ts， $△ P C Q$ 的面积为S，求：

(1)、S与t之间的函数关系式，并写出自变量的取值范围；

(2)、当 $t = 3 s$ 时，求线段PQ的长；

(3)、当t为何值时， $S = \frac{4}{25} S_{△ A B C}$ ？

查看试题解析
23. 如图，直线AB与抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 交于 $A (- 4 ， 0)$ 、 $B (2 ， 6)$ 两点，与y轴交于点C，点D为线段AB上一点，连接OD、OB.

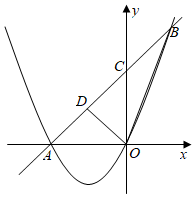(1)、求抛物线的解析式；

(2)、若OD将 $△ A O B$ 分成面积相等的两部分，求点D的坐标；

(3)、在平面坐标内是否存在点P，使得以A、O、B、P为顶点的四边形是平行四边形？若存在，求出点P的坐标；若不存在，请说明理由.

查看试题解析