云南省普洱市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 常见的五角星绕中心旋转一个最小的角度α后，即可与自身重合，则α等于（）

A、90° B、72° C、60° D、180°

查看试题解析
2. 一元二次方程 $x^{2} + 8 x - 9 = 0$ 配方后得到的方程（）

A、 ${(x + 4)}^{2} = 25$ B、 ${(x - 4)}^{2} = 25$ C、 ${(x - 4)}^{2} + 7 = 0$ D、 ${(x + 4)}^{2} - 7 = 0$

查看试题解析
3. 一元二次方程x²+x﹣2=0根的情况是( )

A、有两个不相等的实数根 B、有两个相等的实数根 C、无实数根 D、无法确定

查看试题解析
4. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、等边三角形 B、平行四边形 C、矩形 D、正五边形

查看试题解析
5. 如图①所示，小明将四张牌放在桌上，然后蒙上眼睛，请一位同学上前，将某一张牌旋转180°，小明解开蒙具，看到四张牌如图②所示，他很快就确定被旋转的牌是（）

A、方块4 B、黑桃5 C、梅花6 D、红桃7

查看试题解析
6. 有下列四个命题：
①直径是弦；
②经过三个点一定可以作圆；
③三角形的外心到三角形各顶点的距离都相等；
④半径相等的两个半圆是等弧．
其中正确的有（　　）

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 如图，四边形OABC为菱形，∠AOC＝120°，点B、C在以点O为圆心的 $\overset{⌢}{E F}$ 上，若OA＝1，∠1＝∠2，则扇形OEF的面积为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{4}$ C、 $\frac{π}{3}$ D、 $\frac{2 π}{3}$

查看试题解析
8. 如图，已知AB是⊙O的直径，CD⊥AB于E点，且BC＝6，∠BAC＝30°，则CD的值是（）

A、4 B、 $6 \sqrt{3}$ C、 $8 \sqrt{2}$ D、9.6

查看试题解析

二、填空题

9. 已知x₁、x₂是一元二次方程x²﹣4x+1=0的两个根，则x₁x₂= ．

查看试题解析
10.
如图，AB是⊙O的直径，C是⊙O上一点， $∠ B O C$ =44°，则 $∠ A$ 的度数为．

查看试题解析
11. 某商场在促销活动中，将原价25元的商品，连续两次降价后，现价为16元．则降价率为．

查看试题解析
12. 抛物线 $y = (x - 1)^{2} + 3$ 的顶点坐标是.

查看试题解析
13. ⊙O的半径为1cm，圆心到直线L的距离为1.5cm，则直线L与⊙O的位置关系是

查看试题解析
14. 方程x²＝2x的解是.

查看试题解析
15. 二次函数y＝－3x²＋6x＋9的图象的开口方向，它与y轴的交点坐标是．

查看试题解析

三、解答题

16. 用适当的方法解方程：

(1)、 $x^{2} - 7 x + 6 = 0$

(2)、 $x (5 x + 4) - (5 x + 4) = 0$

查看试题解析
17. 已知△ABC在平面直角坐标系中的位置如图所示．

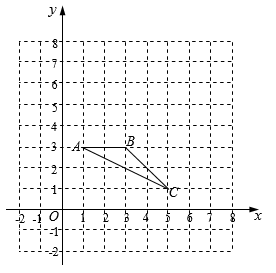(1)、分别写出图中点A和点C的坐标；

(2)、画出△ABC绕点A按逆时针方向旋转90°后的△DEF

查看试题解析
18. 如图，在⊙O中，弦AB与DC相交于E，且AE=EC，求证：AD=BC．

查看试题解析
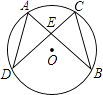19. 某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．

(1)、降价前商品每月销售该商品的利润是多少元？

(2)、要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？

(3)、当这种商品售价定为多少元时，该商品所获的利润最大？最大利润是多少？

查看试题解析
20. 已知抛物线y＝x²＋bx＋c，经过点A（0，5）和点B（3，2）．

(1)、求抛物线的解析式？

(2)、求此抛物线的对称轴及顶点坐标？

查看试题解析
21. 如图，PA、PB是⊙O的两条切线，A、B是切点，AC是⊙O的直径，∠BAC＝35°，求∠P的度数．

查看试题解析
22. 如图，抛物线的顶点坐标D（1，4），且图像与x轴交于A、B两点，A（－1，0）请回答下列问题

(1)、求出抛物线的解析式；

(2)、求抛物线与y轴的交点C的坐标；

(3)、求△ABD的面积？

查看试题解析