上海市闵行区2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-14 类型:期中考试
一、单选题
-
1. 下列各组图形中一定是相似形的是( )A、两个等腰梯形 B、两个矩形 C、两个直角三角形 D、两个等边三角形2. 已知 , 下列式子错误的是( )A、 B、 C、 D、3. 如图,点、分别在的边、上,下列条件中,不能判定的条件是( )
 A、 B、 C、 D、4. 下列有关相似三角形的性质,正确的是( )A、如果两个相似三角形的相似比为 , 那么它们对应角平分线的比为 B、如果两个相似三角形的相似比为 , 那么它们的周长的比为 C、如果两个相似三角形的相似比为 , 那么它们的面积的比为 D、如果两个相似三角形的相似比为 , 那么它们对应中线的比为5. 下列说法中,正确的是( )A、如果 , 则 B、如果和都是单位向量,那么 C、已知与单位向量的方向相反,且长度为3,那么 D、如果 , , 其中是非零向量,那么6. 如图,已知每个小正方形的边长均为1,与的顶点都在小正方形的顶点上,那么与相似的是( )
A、 B、 C、 D、4. 下列有关相似三角形的性质,正确的是( )A、如果两个相似三角形的相似比为 , 那么它们对应角平分线的比为 B、如果两个相似三角形的相似比为 , 那么它们的周长的比为 C、如果两个相似三角形的相似比为 , 那么它们的面积的比为 D、如果两个相似三角形的相似比为 , 那么它们对应中线的比为5. 下列说法中,正确的是( )A、如果 , 则 B、如果和都是单位向量,那么 C、已知与单位向量的方向相反,且长度为3,那么 D、如果 , , 其中是非零向量,那么6. 如图,已知每个小正方形的边长均为1,与的顶点都在小正方形的顶点上,那么与相似的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
7. 在比例尺1:500000的地图上,量得A、B两地的距离为4cm,则A、B两地的实际距离是千米.8. 设点P是线段AB的黄金分割点(AP<BP),AB=4cm,那么线段BP的长是cm.9. 已知两个三角形相似,其中一个三角形的两个内角分别为、 , 则另一个三角形的最大的内角度数为 .10. 一段公路路面的坡度为 , 如果某人沿着这段公路向上行走了130米,那么此人升高了米.11. 如图,已知 , , , , 那么 .
 12. 如图,点是的边上的点, . 设 , , 则 . (用含有和的式子表示)
12. 如图,点是的边上的点, . 设 , , 则 . (用含有和的式子表示) 13. 在中, , , 点是的重心, , 那么的度数为 .14. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为时,梯子顶端靠在墙面上的点处,底端落在水平地面的点处,如果将梯子底端向墙面靠近,使梯子与地面所成角为 , 且 , 则梯子顶端上升了米.
13. 在中, , , 点是的重心, , 那么的度数为 .14. 如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为时,梯子顶端靠在墙面上的点处,底端落在水平地面的点处,如果将梯子底端向墙面靠近,使梯子与地面所成角为 , 且 , 则梯子顶端上升了米. 15. 如图,已知正方形的顶点、在的边上,顶点、分别在边、上,如果 , 边上的高是6,那么这个正方形的边长是 .
15. 如图,已知正方形的顶点、在的边上,顶点、分别在边、上,如果 , 边上的高是6,那么这个正方形的边长是 . 16. 如图,在中,为边的中点,联结 , 与对角线相交于点 , 则与四边形的面积比为 .
16. 如图,在中,为边的中点,联结 , 与对角线相交于点 , 则与四边形的面积比为 . 17. 阅读材料:余弦定理是描述三角形中三边长度与一个角的余弦值关系的定理,是勾股定理在一般三角形情形下的推广.对于任意三角形,任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍.定理解读:如图,在任意中,以边为例,其它两边是和 , 和的夹角为 , 根据余弦定理有 , 类似的可以得到关于和的关系式.已知在中, , , 是和的比例中项,那么的余弦值为 .
17. 阅读材料:余弦定理是描述三角形中三边长度与一个角的余弦值关系的定理,是勾股定理在一般三角形情形下的推广.对于任意三角形,任何一边的平方等于其它两边平方的和减去这两边与它们夹角的余弦的积的两倍.定理解读:如图,在任意中,以边为例,其它两边是和 , 和的夹角为 , 根据余弦定理有 , 类似的可以得到关于和的关系式.已知在中, , , 是和的比例中项,那么的余弦值为 .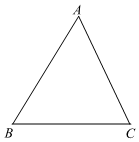 18. 如图,矩形纸片 , , . 如果点在边上,将纸片沿折叠,使点落在点处,如果直线经过点 , 那么线段的长是 .
18. 如图,矩形纸片 , , . 如果点在边上,将纸片沿折叠,使点落在点处,如果直线经过点 , 那么线段的长是 .
三、解答题
-
19. 计算: .20. 如图,已知两个不平行的向量、 . 先化简,再求作: . (不要求写作法,但要指出图中表示结论的向量)
 21. 如图,已知点、分别在中的边、的延长线上,且 .
21. 如图,已知点、分别在中的边、的延长线上,且 . (1)、如果 , , , 求的长;(2)、如果 , , , 过点作 , 垂足为点 , 求的长.22. 如图,楼顶上有一个广告牌AB,从与楼BC相距12米的D处测得广告牌顶部A的仰角为37°,测得广告牌底部B的仰角为30°,求广告牌AB的高度.(结果保留根号,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)、如果 , , , 求的长;(2)、如果 , , , 过点作 , 垂足为点 , 求的长.22. 如图,楼顶上有一个广告牌AB,从与楼BC相距12米的D处测得广告牌顶部A的仰角为37°,测得广告牌底部B的仰角为30°,求广告牌AB的高度.(结果保留根号,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)


