辽宁省锦州市太和区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 用配方法解方程 $x^{2} - 4 x - 3 = 0$ ，下列变形正确的是（）

A、 ${(x - 4)}^{2} = 19$ B、 ${(x - 2)}^{2} = 1$ C、 ${(x - 2)}^{2} = 7$ D、 ${(x + 2)}^{2} = 7$

查看试题解析
2. 在一个不透明的纸箱中，共有15个蓝色、红色的玻璃球，它们除颜色外其他完全相同．小柯每次摸出一个球后放回，通过多次摸球试验后发现摸到蓝色球的频率稳定在20%，则纸箱中红色球很可能有（）

A、3个 B、6个 C、9个 D、12个

查看试题解析
3. 如图，已知四边形ABCD是平行四边形，下列结论中正确的是（）

A、当AB=BC时，它是矩形 B、当AC=BD时，它是菱形 C、当∠ABC=90°时，它是矩形 D、当AC=BD时，它是正方形

查看试题解析
4. 如图，在菱形 $A B C D$ 中，若 $A B = 5 ， A C = 8$ ，则点D到 $B C$ 的距离为（）

A、 $\frac{12}{5}$ B、 $\frac{24}{5}$ C、 $\frac{48}{5}$ D、5

查看试题解析
5. 如图，在矩形 $A B C D$ 中， $A C$ ， $B D$ 相交于点O，若 $Δ A O B$ 的面积是3，则矩形 $A B C D$ 的面积是（）

A、 $6$ B、 $9$ C、 $12$ D、 $15$

查看试题解析
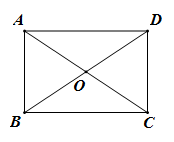6. 若关于x的一元二次方程k $x^{2}$ -6x+9=0有两个不相等的实数根，则k的取值范围是（）

A、k<1 B、k<1且k≠0 C、k≠1 D、k>1

查看试题解析
7. 如图，在△ABC中，∠ACB＝90°，∠B＝40°，分别以点A和点B为圆心，以相同的长（大于 $\frac{1}{2}$ AB）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交BC于点E，连接CD，则∠CDE等于（）

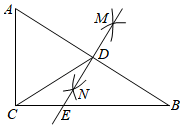A、8° B、10° C、15° D、20°

查看试题解析
8. 如图，正方形ABCD中，E，F分别为AB，AD上的点，AF＝BE，CE，BF交于点H，BF交AC于点M，O为AC的中点，OB交CE于点N，连接OH．下列结论：①BF⊥CE；②BM＝CN；③∠FHO＝45°；④CH﹣BH＝ $\sqrt{2}$ OH，正确的个数（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

9. 若方程（m﹣2） $x^{m^{2} - 2}$ ﹣2x﹣4＝0是关于x的一元二次方程，则m＝．

查看试题解析
10. 方程 $x (x - 3) - 5 (x - 3) = 0$ 的根是．

查看试题解析
11. 某型号手机连续两次降价后，由原来的1225元降为625元，设平均每次降价的百分率为x，根据题意列方程为．

查看试题解析
12. 一天晚上，小伟帮妈妈清洗茶杯，三个茶杯只有颜色不同，其中一个无盖，突然停电了，小伟只好把杯盖与茶杯随机地搭配在一起，则花色完全搭配正确的概率是.

查看试题解析
13. 如图，菱形ABCD的顶点C在直线MN上，若∠1＝50°，∠2＝20°，则∠BDC的度数为．

查看试题解析
14. 有两个全等矩形纸条，长与宽分别为10和6，按如图所示的方式交叉叠放在一起，则重合部分构成的四边形BGDH的周长为．

查看试题解析
15. 如图，正方形ABCD和正方形AEFG的边长分别为5 cm和3 cm，点E、G分别为AB、AD边上的点，H为CF的中点，连接HG，则HG的长为．

查看试题解析
16. 如下图，在平面直角坐标系中有一边长为l的正方形OABC，边OA、OC分别在x轴、y 轴上，如果以对角线OB为边作第二个正方形OBB₁C₁ ，再以对角线OB_l为边作第三个正方形OB_lB₂C₂ ，照此规律作下去，则点B₂₀₂₀的纵坐标为。

查看试题解析

三、解答题

17. 用适当的方法解方程

(1)、x²﹣2x﹣5＝0；（用配方法）

(2)、x²﹣2 $\sqrt{5}$ x﹣4＝0；（用公式法）

(3)、（x+1）²＝3（x+1）；（用因式分解法）

(4)、2x²+3x＝1．（选择适当的方法）

查看试题解析
18. 某品牌免洗洗手液按剂型分为凝胶型、液体型，泡沫型三种型号（分别用A，B，C依次表示这三种型号）．小辰和小安计划每人购买一瓶该品牌免洗洗手液，上述三种型号中的每一种免洗洗手液被选中的可能性均相同．

(1)、小辰随机选择一种型号是凝胶型免洗洗手液的概率是．

(2)、请你用列表法或画树状图法，求小辰和小安选择同一种型号免洗洗手液的概率．

查看试题解析
19. 如图，△ABC中，∠BCA＝90°，CD是边AB上的中线，分别过点C，D作BA和BC的平行线，两线交于点E，且DE交AC于点O，连接AE．

(1)、求证：四边形ADCE是菱形；

(2)、若∠B＝60°，BC＝6，求四边形ADCE的面积．

查看试题解析
20. 如图，在△ABC中，点D，E分别是AB，AC的中点，连接ED并延长至点F，使DF＝DE，连接AF，BF，BE.

(1)、求证：△ADE≌△BDF.

(2)、若∠ABE＝∠CBE，求证：四边形AFBE是矩形.

查看试题解析
21. 某学校计划利用一片空地建一个学生自行车车棚，其中一面靠墙，这堵墙的长度为12米.计划建造车棚的面积为80平方米，已知现有的木板材料可使新建板墙的总长为28米.

(1)、这个车棚的长和宽分别应为多少米？

(2)、如图，为了方便学生取车，施工单位决定在车棚内修建几条等宽的小路，使得停放自行车的面积为54平方米，那么小路的宽度是多少米？

查看试题解析
22. 列方程（组）解应用题
端午节期间，某水果超市调查某种水果的销售情况，下面是调查员的对话：

小王：该水果的进价是每千克22元；

小李：当销售价为每千克38元时，每天可售出160千克；若每千克降低3元，每天的销售量将增加120千克．

根据他们的对话，解决下面所给问题：超市每天要获得销售利润3640元，又要尽可能让顾客得到实惠，求这种水果的销售价为每千克多少元？

查看试题解析
23. 已知：如图，在边长为1的正方形ABCD中，点P是对角线AC上的一个动点（与点A、C不重合），过点P作 $P E ⊥ P B$ ，PE交边CD于点E ，过点E作 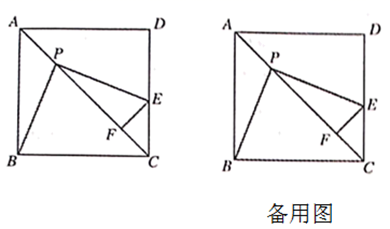$E F ⊥ A C$ ，垂足为F ．

(1)、求证： $P B = P E$ ；

(2)、在点P的运动过程中，PF的长度是否发生变化？若不变，试求出这个不变的值，写出解答过程；若变化，试说明理由．

查看试题解析