辽宁省丹东市东港市2021-2022学年九年级上学期期中数学试题
试卷更新日期：2022-09-14 类型：期中考试
一、单选题
-
1. 若x2﹣3x的值等于零，则x的值为（ ）A、﹣3 B、0 C、0或3 D、0或﹣32. 若 ， a﹣b+c＝18，则a的值为（ ）A、11 B、12 C、13 D、143. 若两个等腰直角三角形斜边的比是1：3，则它们的面积比是（ ）A、1：4 B、1：6 C、1：9 D、1：104. 三角形两边的长是2和4，第三边的长是方程x2﹣12x+35＝0的根，则该三角形的周长为（ ）A、11 B、13 C、11或13 D、以上都不对5. 如图，P是直角△ABC斜边AB上任意一点（A，B两点除外），过点P作一条直线，使截得的三角形与△ABC相似，这样的直线可以作（ ）
A、4条 B、3条 C、2条 D、1条6. 如图，已知正方形ABCD的边长为6，点E，F分别在边AB，BC上，BE＝CF＝2，CE与DF交于点H，点G为DE的中点，连接GH，则GH的长为（ ）
A、 B、 C、4.5 D、4.37. 如图，在▱ABCD中，对角线AC，BD相交于点O，在DC的延长线上取一点E，连接OE交BC于点F，若AB＝4，BC＝6，CE＝1，则CF的长为（ ）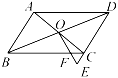
A、 B、1.5 C、 D、18. 如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连接BD、DP，BD与CF交于点H．下列结论：①CF＝2AE；②△DFP∽△BPH；③DP2＝PH•PC；④PE：BC＝（2﹣3）：3．正确的有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
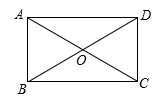
9. 一个不透明的口袋中装有10个黑球和若干个白球，小球除颜色外其余均相同，从中随机摸出一球记下颜色，再放回袋中，不断重复上述过程，一共摸了150次，其中有50次摸到黑球，由此估计口袋中白球的个数约为 个．10. 已知线段AB＝4cm，C是AB的黄金分割点，且AC＞BC，则AC＝ ．11. 若关于的一元二次方程有实根，则的取值范围是12. 如图，矩形ABCD的两条对角线AC，BD交于点O，∠AOB＝60°，AB＝3，则矩形的周长为 ．
13. 某超市第二季度的营业额为200万元，第四季度的营业额为288万元．如果每季度营业额的平均增长率相同，那么每季度的平均增长率为 ．14. 如图，菱形ABCD的周长为16cm，BC的垂直平分线EF经过点A，则对角线BD长为cm．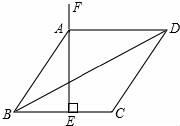
15. 如图，正方形ABCD的面积为18，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为 ．
16. 如图，依次连接第一个矩形各边的中点得到一个菱形，再依次连接菱形各边的中点得到第二个矩形，按照此方法继续下去.已知第一个矩形的面积为1，则第n个矩形的面积为.
三、解答题
-
17. 计算：(1)、3x2+3＝7x；（用配方法解方程）(2)、4y（3﹣y）＝（y﹣3）2 ．18. 如图在平面直角坐标系中，△ABC的位置如图所示，顶点坐标分别为：A（﹣2，0），B（﹣3，2），C（﹣1，1）．
⑴做出△ABC关于y轴对称的图形△A1B1C1；
⑵以原点O为位似中心，在y轴右侧画出△ABC的位似图形△A2B2C2 ， 使它与△ABC的相似比是2：1；
⑶若M（x，y）是线段AB上一点，则点M关于y轴对称的对应点M1的坐标为 ▲ ．
19. 为了参加全市中学生“党史知识竞赛”，某校准备从甲、乙2名女生和丙、丁2名男生中任选2人代表学校参加比赛.(1)、如果已经确定女生甲参加，再从其余的候选人中随机选取1人，则女生乙被选中的概率是；(2)、求所选代表恰好为1名女生和1名男生的概率.20. 某商场以每件280元的价格购进一批商品，当每件商品售价为360元时，每月可售出60件，为了扩大销售，商场决定采取适当降价的方式促销，经调查发现，如果每件商品降价1元，那么商场每月就可以多售出5件．要使商场每月销售这种商品的利润达到7200元，且更有利于减少库存，则每件商品应降价多少元？21. 如图，△ABC中，AB=AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE=OD，连接AE，BE．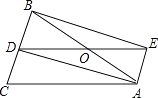
(1)、求证：四边形AEBD是矩形；(2)、当△ABC满足什么条件时，矩形AEBD是正方形，并说明理由22. 如图，在▱ABCD中，对角线AC，BD交于点O，E是BD延长线上一点，且△ACE是等边三角形．
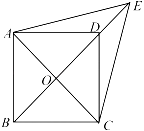(1)、求证：四边形ABCD是菱形；(2)、若∠AED＝2∠EAD，AB＝a，求四边形ABCD的面积．23. 如图，△ABD中，∠A＝90°，AB＝6cm，AD＝12cm．某一时刻，动点M从点A出发沿AB方向以1cm/s的速度向点B匀速运动；同时，动点N从点D出发沿DA方向以2cm/s的速度向点A匀速运动，运动的时间为ts．
(1)、求t为何值时，△AMN的面积是△ABD面积的；(2)、当以点A，M，N为顶点的三角形与△ABD相似时，求t值．24. 如图，过矩形ABCD（AD＞AB）的对角线AC的中点O作AC的垂直平分线EF，分别交AD、BC于点E、F，分别连接AF和CE．
(1)、判断四边形AFCE是什么特殊四边形，并证明；(2)、过点E作AD的垂线交AC于点P，求证：2AE2＝AC•AP．25. 在四边形ABCD中，对角线AC、BD相交于点O，将△COD绕点O按逆时针方向旋转得到△C1OD1 ， 旋转角为α（0°＜α＜90°），连接AC1、BD1 ， AC1与BD1交于点P．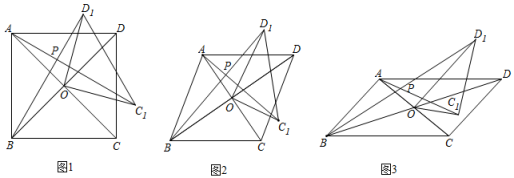
(1)、如图1，若四边形ABCD是正方形．①求证：△AOC1≌△BOD1；
②请直接写出AC1与BD1的位置关系；
(2)、如图2，若四边形ABCD是菱形，AC＝3，BD＝5，设AC1＝kBD1 ． 判断AC1与BD1的位置关系，请说明理由，并求出k的值．(3)、如图3，若四边形ABCD是平行四边形，AC＝6，BD＝12，连接DD1 ， 设AC1＝kBD1 ． 请直接写出k的值和AC12+（kDD1）2的值．