辽宁省鞍山市台安县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-14 类型:期中考试
一、单选题
-
1. 若方程(m﹣2)x|m|+3mx+1=0是关于x的一元二次方程,则m的值为( )A、±2 B、+2 C、﹣2 D、以上都不对2. 下列关于防范“新冠肺炎”的标志中既是轴对称图形,又是中心对称图形的是( )A、
 戴口罩讲卫生
B、
戴口罩讲卫生
B、 勤洗手勤通风
C、
勤洗手勤通风
C、 有症状早就医
D、
有症状早就医
D、 少出门少聚集
3. 下列说法正确的是( )A、平分弦的直径垂直于弦 B、等弧所对的圆心角相等 C、经过三点可以做一个圆 D、三角形的外心到三角形三边的距离相等4. 函数y=ax2﹣2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )A、
少出门少聚集
3. 下列说法正确的是( )A、平分弦的直径垂直于弦 B、等弧所对的圆心角相等 C、经过三点可以做一个圆 D、三角形的外心到三角形三边的距离相等4. 函数y=ax2﹣2x+1和y=ax+a(a是常数,且a≠0)在同一直角坐标系中的图象可能是( )A、 B、
B、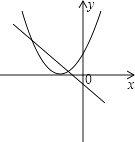 C、
C、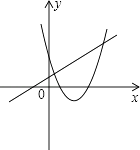 D、
D、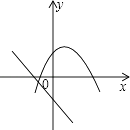 5. 将抛物线y=﹣2(x+1)2﹣3先向右平移4个单位长度,再向上平移5个单位长度,得到的抛物线的函数表达式是( )A、y=﹣2(x﹣5)2+8 B、y=﹣2(x﹣3)2+8 C、y=﹣2(x﹣5)2+2 D、y=﹣2(x﹣3)2+26. 如图,△ODC是由△OAB绕点O顺时针旋转40°后得到的图形,若点D恰好落在AB上,且∠AOC=100°,则∠C的度数是( )
5. 将抛物线y=﹣2(x+1)2﹣3先向右平移4个单位长度,再向上平移5个单位长度,得到的抛物线的函数表达式是( )A、y=﹣2(x﹣5)2+8 B、y=﹣2(x﹣3)2+8 C、y=﹣2(x﹣5)2+2 D、y=﹣2(x﹣3)2+26. 如图,△ODC是由△OAB绕点O顺时针旋转40°后得到的图形,若点D恰好落在AB上,且∠AOC=100°,则∠C的度数是( ) A、50° B、60° C、65° D、70°7. 如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( )
A、50° B、60° C、65° D、70°7. 如图,△ABC中,∠C=90°,AC=12,BC=5,⊙O与△ABC的三边相切于点D、E、F,则AD长为( ) A、8 B、10 C、12 D、148. 二次函数y=ax2+bx+c(a≠0)的图象的一部分如图所示.已知图象经过点(3,0),对称轴为直线x=1,现给出下列结论:①abc<0;②a﹣b+c=0;③8a+c<0;④若抛物线经过点(﹣3,n),则关于x的一元二次方程ax2+bx+c﹣n=0(a≠0)的两根分别为﹣3,5.上述结论中正确结论的个数为( )
A、8 B、10 C、12 D、148. 二次函数y=ax2+bx+c(a≠0)的图象的一部分如图所示.已知图象经过点(3,0),对称轴为直线x=1,现给出下列结论:①abc<0;②a﹣b+c=0;③8a+c<0;④若抛物线经过点(﹣3,n),则关于x的一元二次方程ax2+bx+c﹣n=0(a≠0)的两根分别为﹣3,5.上述结论中正确结论的个数为( ) A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
9. 已知抛物线y=ax2的开口向上,且|a|=4,则a= .10. 若a是方程x2﹣2x﹣3=0的一个根,则代数式2021﹣a2+2a的值为 .11. 三角形两边的长分别为3和6,第三边的长是方程x2﹣9x+18=0的根,则该三角形的周长为 .12. 已知点A(1,y1),B(2,y2),C(﹣2,y3)在抛物线y=﹣(x+1)2+n上,则y1 , y2 , y3的大小关系是 (用“<”连接).13. 一个已知点P到圆周上的最长距离是9,最短距离是3,则此圆的半径是 .14. 某商店连续两次降价10%后商品的价格是81元,则该商品原来的价格是元15. 如图,⊙O的弦AC=BD,且AC⊥BD于点E,连接AB,若⊙O的半径是3cm,则AB的长是 cm.
 16. 如图,在⊙O中,直径AB=2,延长AB至C,使BC=OB,点D在⊙O上运动,连接CD,将CD绕点C顺时针旋转90°得到CE,连接OE,则线段OE的最大值为 .
16. 如图,在⊙O中,直径AB=2,延长AB至C,使BC=OB,点D在⊙O上运动,连接CD,将CD绕点C顺时针旋转90°得到CE,连接OE,则线段OE的最大值为 .
三、解答题
-
17. 按照要求解方程:(1)、x2﹣2x﹣8=0(配方法);(2)、5x2﹣3x=x+1(公式法).18. △ABC在平面直角坐标系中的位置如图所示,A、B、C三点在格点上.

⑴画出△ABC关于x轴对称的△A1B1C1;
⑵画出△ABC绕点O按逆时针方向旋转90°后的△A2B2C2;
⑶连接A1、A2 , 并直接写出线段A1A2的长.
19. 关于x的一元二次方程(m﹣1)x2﹣x﹣2=0(1)、若x=﹣1是方程的一个根,求m的值及另一个根.(2)、当m为何值时方程有两个不同的实数根.20. 为满足市场需求,中百超市在中秋节前夕购进价格为6元/个的月饼,根据市场预测,该品牌月饼每个售价8元时,每天能出售1000个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌月饼的售价不能超过进价的200%.(1)、该品牌月饼每个售价为9元,则每天出售多少个?(2)、该品牌月饼定价为多少元时,该超市每天的销售利润为3200元.21. 如图,⊙O中两条互相垂直的弦AB,CD交于点E. (1)、点G是CD的中点,OG=3,CD=8,求⊙O的半径长;(2)、点F在CD上,且CE=EF,求证:AF⊥BD.22. 某幢建筑物从10米高的窗户A用水管向外喷水,喷出的水流呈抛物线状(如图),若抛物线最高点M离墙1米,离地面 米.问:
(1)、点G是CD的中点,OG=3,CD=8,求⊙O的半径长;(2)、点F在CD上,且CE=EF,求证:AF⊥BD.22. 某幢建筑物从10米高的窗户A用水管向外喷水,喷出的水流呈抛物线状(如图),若抛物线最高点M离墙1米,离地面 米.问: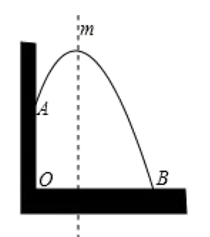 (1)、求抛物线的解析式;(2)、求水流落地点B离墙的距离23. 如图,AB为⊙O的切线,B为切点,过点B作BC⊥OA,垂足为点E,交⊙O于点C,连接CO并延长CO与AB的延长线交于点D,连接AC.
(1)、求抛物线的解析式;(2)、求水流落地点B离墙的距离23. 如图,AB为⊙O的切线,B为切点,过点B作BC⊥OA,垂足为点E,交⊙O于点C,连接CO并延长CO与AB的延长线交于点D,连接AC. (1)、求证:AC为⊙O的切线;(2)、若⊙O半径为2,OD=4.求线段AD的长.24. 小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现:每月的销售量y(件)与销售单价x(元/件)之间的关系可近似地看作一次函数y=-10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.(1)、设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元/件)之间的函数表达式,并确定自变量x的取值范围;(2)、当销售单价定为多少元/件时,每月可获得最大利润?每月的最大利润是多少?25. 在△ABC中,AB=AC,D是边BC上一动点,连接AD,将AD绕点A逆时针旋转至AE的位置,使得∠DAE+∠BAC=180°.
(1)、求证:AC为⊙O的切线;(2)、若⊙O半径为2,OD=4.求线段AD的长.24. 小明投资销售一种进价为每件20元的护眼台灯.销售过程中发现:每月的销售量y(件)与销售单价x(元/件)之间的关系可近似地看作一次函数y=-10x+500,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.(1)、设小明每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元/件)之间的函数表达式,并确定自变量x的取值范围;(2)、当销售单价定为多少元/件时,每月可获得最大利润?每月的最大利润是多少?25. 在△ABC中,AB=AC,D是边BC上一动点,连接AD,将AD绕点A逆时针旋转至AE的位置,使得∠DAE+∠BAC=180°. (1)、如图1,当∠BAC=90°时,连接BE,交AC于点F,若BE平分 , BD=2,求AF的长;(2)、如图2,连接BE,取BE的中点G,连接AG,猜想AG与CD存在的数量关系,并证明你的猜想;(3)、如图3,在(2)的条件下,连接DG,CE.若 , 当BD>CD,∠AEC=150°时,请直接写出的值.26. 如图,抛物线y=ax²+bx+3与x轴交于点A(3,0),B(1,0),与y轴交于点C.
(1)、如图1,当∠BAC=90°时,连接BE,交AC于点F,若BE平分 , BD=2,求AF的长;(2)、如图2,连接BE,取BE的中点G,连接AG,猜想AG与CD存在的数量关系,并证明你的猜想;(3)、如图3,在(2)的条件下,连接DG,CE.若 , 当BD>CD,∠AEC=150°时,请直接写出的值.26. 如图,抛物线y=ax²+bx+3与x轴交于点A(3,0),B(1,0),与y轴交于点C. (1)、求抛物线的解析式;(2)、D为抛物线上一点,且不与点B重合,若S△ACD=S△ABC,求点D的坐标;(3)、E为抛物线上一点,若∠BCE=45°,求点E的坐标.
(1)、求抛物线的解析式;(2)、D为抛物线上一点,且不与点B重合,若S△ACD=S△ABC,求点D的坐标;(3)、E为抛物线上一点,若∠BCE=45°,求点E的坐标.