黑龙江省同江市六校2021-2022学年九年级上学期期中考试数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、填空题

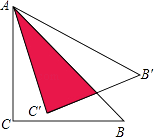
1. 盐通铁路沿线水网密布，河渠纵横，将建设特大桥梁6座，桥梁的总长度约为146000米，将数据146000用科学记数法表示为.

查看试题解析
2. 函数y= $\frac{\sqrt{x + 2}}{x}$ 中，自变量x的取值范围是．

查看试题解析
3. 设点（﹣1，y₁），（2，y₂），（3，y₃）是抛物线y=﹣x²+a上的三点，则y₁、y₂、y₃的从小到大排列为.

查看试题解析
4. 关于x的方程（a﹣6）x²﹣8x+6=0有实数根，则a的取值范围是．

查看试题解析
5. 将抛物线 $y = x^{2} - 4 x - 4$ 向左平移3个单位，再向上平移5个单位，得到抛物线的表达式为.

查看试题解析
6. 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后，得到△AB′C′，则图中阴影部分的面积是 cm² ．

查看试题解析
7. 如图，在△ABC中，∠C=90°，AC=4，BC=3，将△ABC绕点A逆时针旋转，使点C落在线段AB上的点E处，点B落在点D处，则BD的长为.

查看试题解析
8. 已知三角形两边的长分别是8和 $6$ ，第三边的长是一元二次方程 $x^{2} - 16 x + 60 = 0$ 的一个实数根，则该三角形的面积是．

查看试题解析
9. 抛物线y=ax²+bx+c（a≠0）的对称轴是直线x=1，且经过点A（3，0），则a﹣b+c的值为.

查看试题解析
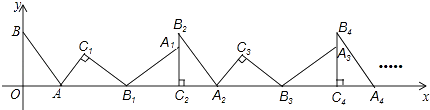
10.
如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB₁C₁的位置，点B、O分别落在点B₁、C₁处，点B₁在x轴上，再将△AB₁C₁绕点B₁顺时针旋转到△A₁B₁C₂的位置，点C₂在x轴上，将△A₁B₁C₂绕点C₂顺时针旋转到△A₂B₂C₂的位置，点A₂在x轴上，依次进行下去…．若点A（ $\frac{3}{2}$ ，0），B（0，2），则点B₂₀₁₆的坐标为．

查看试题解析

二、单选题

11. 下面四个图标中，属于中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
12. 已知a<0，则点P(-a² ， -a+1)关于原点的对称点P′在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析

13. 二次函数图象上部分点的坐标对应值列表如下：

x	…	﹣3	﹣2	﹣1	0	1	…
y	…	﹣3	﹣2	﹣3	﹣6	﹣11	…

则该函数图象的对称轴是（）

A、直线x＝﹣3 B、直线x＝﹣2 C、直线x＝﹣1 D、直线x＝0

查看试题解析

14. 关于函数y=2x²﹣4x，下列叙述中错误的是（）

A、函数图象经过原点 B、函数图象的最低点是（1，﹣2） C、函数图象与x轴的交点为（0，0），（2，0） D、当x＞0时，y随x的增大而增大

查看试题解析
15. 在□ABCD中，AB=10，BC=14，E，F分别为边BC，AD上的点，若四边形AECF为正方形，则AE的长为（）

A、7 B、4或10 C、5或9 D、6或8

查看试题解析
16. 当ab>0时，y=ax²与y=ax+b的图象大致是（）

A、 B、 C、 D、

查看试题解析
17. 已知抛物线y＝x²+bx+c的部分图象如图所示，若y＜0，则x的取值范围是（）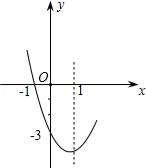

A、﹣1＜x＜4 B、﹣1＜x＜3 C、x＜﹣1或x＞4 D、x＜﹣1或x＞3

查看试题解析
18. 如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A₁B₁C，连接AA₁ ，若∠AA₁B₁＝15°，则∠B的度数是（）

A、75° B、60° C、50° D、45°

查看试题解析
19.
二次函数y=ax²+bx+c（a≠0）的图象如图所示，对称轴为x=1，给出下列结论：①abc＞0；②b²=4ac；③4a+2b+c＞0；④3a+c＞0，其中正确的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
20. 在等边 $△ A B C$ 中， $D$ 是边 $A C$ 上一点，连接 $B D$ ，将 $△ B C D$ 绕点 $B$ 逆时针旋转 $6 0^{∘}$ ，得到 $△ B A E$ ，连接 $E D$ ，若 $B C = 5$ ， $B D = 4$ ，有下列结论：① $A E ∥ B C$ ；② $∠ A D E = ∠ B D C$ ；③ $△ B D E$ 是等边三角形；④ $△ A D E$ 的周长是 $9$ ．其中，正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

三、解答题

21. 先化简、再求值： $(1 - \frac{1}{x + 1}) \div \frac{x}{x^{2} - 1}$ ，其中 $x = \sqrt{2} + 1$ ．

查看试题解析
22. 如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B（4，1），C（3，3）．
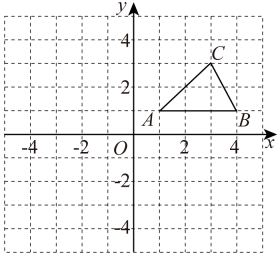
⑴将△ABC向下平移5个单位后得到△A₁B₁C₁ ，请画出△A₁B₁C₁；
⑵将△ABC绕原点O逆时针旋转90°后得到△A₂B₂C₂ ，请画出△A₂B₂C₂；
⑶判断以O，A₁ ， B为顶点的三角形的形状．（无须说明理由）

查看试题解析
23. 已知：二次函数图象的顶点坐标是(3，5)，且抛物线经过点A(1，3).

(1)、求此抛物线的表达式；

(2)、如果点A关于该抛物线对称轴的对称点是B点，且抛物线与y轴的交点是C点，求△ABC的面积.

查看试题解析
24. 海静中学开展以“我最喜爱的职业”为主题的调查活动，围绕“在演员、教师、医生、律师、公务员共五类职业中，你最喜爱哪一类？（必选且只选一类）”的问题，在全校范围内随机抽取部分学生进行问卷调查，将调查结果整理后绘制成如图所示的不完整的统计图，请你根据图中提供的信息回答下列问题：

(1)、本次调查共抽取了多少名学生？

(2)、求在被调查的学生中，最喜爱教师职业的人数，并补全条形统计图；

(3)、若海静中学共有1500名学生，请你估计该中学最喜爱律师职业的学生有多少名？

查看试题解析
25. 小玲和弟弟小东分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30min.小东骑自行车以300m/min的速度直接回家，两人离家的路程y（m）与各自离开出发地的时间x（min）之间的函数图象如图所示

(1)、家与图书馆之间的路程为多少m，小玲步行的速度为多少m/min；

(2)、求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；

(3)、求两人相遇的时间.

查看试题解析
26. 将两块斜边长相等的等腰直角三角板按如图①摆放，斜边AB分别交CD，CE于M，N点．

(1)、如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF，连接FM，如图②，求证：△CMF≌△CMN；

(2)、将△CED绕点C旋转，则：
①当点M，N在AB上(不与点A，B重合)时，线段AM，MN，NB之间有一个不变的关系式，请你写出这个关系式，并说明理由；

②当点M在AB上，点N在AB的延长线上(如图③)时，①中的关系式是否仍然成立？

查看试题解析
27. “扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为30元/件，每天销售量 $y$ （件）与销售单价 $x$ （元）之间存在一次函数关系，如图所示.

(1)、求 $y$ 与 $x$ 之间的函数关系式；

(2)、如果规定每天漆器笔筒的销售量不低于240件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？

(3)、该网店店主热心公益事业，决定从每天的销售利润中捐出150元给希望工程，为了保证捐款后每天剩余利润不低于3600元，试确定该漆器笔筒销售单价的范围.

查看试题解析
28. 如图，四边形OABC是矩形，点A、C在坐标轴上，△ODE是由△OCB绕点O顺时针旋转90°得到的，点D在X轴上，直线BD交Y轴于点F，交OE于点H，线段BC、OC的长是方程x2-6x+8=0的两个根，且OC＞BC．

(1)、求直线BD的解析式.

(2)、求 △OFH的面积.

(3)、点M在坐标轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由.

查看试题解析