黑龙江省绥化市绥棱县2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-14 类型:期中考试
一、单选题
-
1. 下列方程是关于的一元二次方程的是( )A、 B、 C、 D、2. 已知关于的方程的一个根为 , 则实数的值为A、1 B、﹣1 C、2 D、﹣23. 一元二次方程的解是( )A、 B、 C、 , D、4. 下列图象中,是二次函数的图象的是( )A、
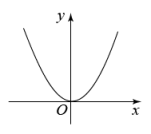 B、
B、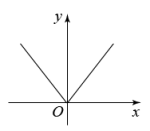 C、
C、 D、
D、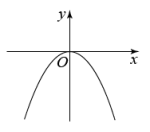 5. 关于的一元二次方程的根的情况( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 若是一元二次方程的两根,则的值为( )A、-5 B、5 C、-4 D、47. 对于函数 , 以下四种说法中正确的是( )A、当时,它是一次函数 B、当时,它是二次函数 C、当时,它是二次函数 D、以上说法都不对8. 若方程的左边可以写成一个完全平方式,则的值为( )A、-2 B、-2或6 C、-2或-6 D、2或-69. 已知点 , , 都在函数的图象上,则( )A、 B、 C、 D、10. 某种火箭竖直向上发射时,它的高度与时间的关系可以用表示,则经过多长时间,火箭达到它的最高点( )A、12s B、13s C、14s D、15s
5. 关于的一元二次方程的根的情况( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定6. 若是一元二次方程的两根,则的值为( )A、-5 B、5 C、-4 D、47. 对于函数 , 以下四种说法中正确的是( )A、当时,它是一次函数 B、当时,它是二次函数 C、当时,它是二次函数 D、以上说法都不对8. 若方程的左边可以写成一个完全平方式,则的值为( )A、-2 B、-2或6 C、-2或-6 D、2或-69. 已知点 , , 都在函数的图象上,则( )A、 B、 C、 D、10. 某种火箭竖直向上发射时,它的高度与时间的关系可以用表示,则经过多长时间,火箭达到它的最高点( )A、12s B、13s C、14s D、15s二、填空题
-
11. 二次函数开口方向是 .12. 当 时,关于的一元二次方程无实数根.13. 若关于的方程是一元二次方程,则 .14. 某快递公司十月份快递件数是10万件,如果该公司第四季度每个月快递件数的增长率都为x(x>0),十二月份的快递件数为y万件,那么y关于x的函数解析式是 .15. 把抛物线向左平移3个单位长度,再向下平移7个单位长度,得到的抛物线解析式为 .16. 抛物线 , 若其顶点在x轴上,则 .17. 一个三角形的两边长分别为3和6,第三边长是方程x2-10x+21=0的根,则三角形的周长为.18. 已知 、 是方程 的两根,则 .19. 已知二次函数的图象如图所示,下列结论:①;②;③;④ , 正确的是 .
 20. 已知某人卖盒饭的盒数个与所获利润元满足关系式 , 则当卖出盒饭数量为盒时,获得最大利润元.
20. 已知某人卖盒饭的盒数个与所获利润元满足关系式 , 则当卖出盒饭数量为盒时,获得最大利润元.三、解答题
-
21. 已知关于x的方程x2﹣(2k+1)x+k2+k=0.(1)、求证:无论k为任何实数值,方程总有两个不相等的实数根;(2)、若两实数根x1、x2满足(x1+1)(x2+1)=12,求k的值.22. 解方程(1)、;(2)、;(3)、;(4)、23. 如图:在平面直角坐标系中,网格中每一个小正方形的边长是1个单位长度,已知 .

⑴将向轴负方向平移5个单位得;
⑵以为旋转中心,将顺时针旋转得;画出平移和旋转后的图形,并写出对应字母的坐标.
24. 某班级的一个小组同学每两个都握手一次,共握手66次,求该小组共有多少人?25. 已知抛物线是常数的对称轴是直线(1)、求证:;(2)、若关于的一元二次方程的一个根为 , 求方程的另一个根.26. 如图,将绕点顺时针旋转得到 , 使点的对应点落在边上,点的对应点为 , 连接 , 证明: .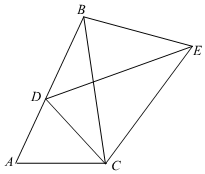 27. 如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.
27. 如图,二次函数y=(x﹣2)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点.已知一次函数y=kx+b的图象经过该二次函数图象上点A(1,0)及点B.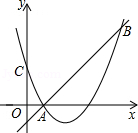 (1)、求二次函数与一次函数的解析式;(2)、根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.28. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少元?(3)、若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
(1)、求二次函数与一次函数的解析式;(2)、根据图象,写出满足kx+b≥(x﹣2)2+m的x的取值范围.28. 某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.(1)、求y与x之间的函数关系式;(2)、当每件售价定为多少元时,每星期的销售利润最大,最大利润是多少元?(3)、若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?