黑龙江省佳木斯市抚远市2021-2022学年九年级上学期期中数学试题
试卷更新日期:2022-09-14 类型:期中考试
一、填空题
-
1. 一元二次方程的解为 .2. 已知抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点.若点A的坐标为(-2,0),抛物线的对称轴为直线x=2,则线段AB的长为 .3. 关于x的一元二次方程(a﹣1)x2﹣2x+3=0有实数根,则整数a的最大值是 .4.
如图,两块相同的三角板完全重合在一起,∠A=30°,AC=10,把上面一块绕直角顶点B逆时针旋转到△A′BC′的位置,点C′在AC上,A′C′与AB相交于点D,则C′D=
 5. 抛物线y=2(x﹣2)2﹣7的顶点为C,若函数y=﹣kx﹣3的图象经过点C,则它与两坐标轴所围成的三角形的面积为 .6. 三角形两边的长分别是8和6,第三边的长是一元二次方程 的一个实数根,则该三角形的面积是 .7. 把抛物线图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是 .8. 已知二次函数 ,若 ,则y的取值范围为.9. 如图,正方形ABCD中,已知AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,则△AEF的面积为 .
5. 抛物线y=2(x﹣2)2﹣7的顶点为C,若函数y=﹣kx﹣3的图象经过点C,则它与两坐标轴所围成的三角形的面积为 .6. 三角形两边的长分别是8和6,第三边的长是一元二次方程 的一个实数根,则该三角形的面积是 .7. 把抛物线图象向左平移2个单位,再向上平移3个单位,所得的抛物线的函数关系式是 .8. 已知二次函数 ,若 ,则y的取值范围为.9. 如图,正方形ABCD中,已知AB=3,点E,F分别在BC、CD上,且∠BAE=30°,∠DAF=15°,则△AEF的面积为 . 10. 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2020次,点P依次落在点P1 , P2 , P3 , P4 , …,P2020的位置,则P2020的横坐标x2020=
10. 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2020次,点P依次落在点P1 , P2 , P3 , P4 , …,P2020的位置,则P2020的横坐标x2020=
二、单选题
-
11. 下列图形是我国国产品牌汽车的标识,在这些汽车标识中,是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 12. 已知函数 y=(m+2)是二次函数,则 m 等于( )A、±2 B、2 C、-2 D、±13. 下列抛物线中,过原点的抛物线是( )A、y=x2﹣1 B、y=(x+1)2 C、y=x2+x D、y=x2﹣x﹣114. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C , 连接AA',若∠1=25°,则∠BAA'的度数是( )
12. 已知函数 y=(m+2)是二次函数,则 m 等于( )A、±2 B、2 C、-2 D、±13. 下列抛物线中,过原点的抛物线是( )A、y=x2﹣1 B、y=(x+1)2 C、y=x2+x D、y=x2﹣x﹣114. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A'B'C , 连接AA',若∠1=25°,则∠BAA'的度数是( )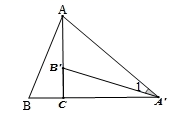 A、70° B、65° C、60° D、55°15. 设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=(x-1)2-3上的三点,则y1 , y2 , y3的大小关系为( )A、 B、 C、 D、16. 如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( )
A、70° B、65° C、60° D、55°15. 设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=(x-1)2-3上的三点,则y1 , y2 , y3的大小关系为( )A、 B、 C、 D、16. 如图所示的容器内装满水,打开排水管,容器内的水匀速流出,则容器内液面的高度h随时间x变化的函数图象最接近实际情况的是( ) A、
A、 B、
B、 C、
C、 D、
D、 17. 如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为 , 求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( )
17. 如图,在宽为20m,长为32m的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为 , 求道路的宽.如果设小路宽为x,根据题意,所列方程正确的是( ) A、 B、 C、 D、18. 九年级(1)班的全体同学,在新年来临之际,在贺卡上写上自己的心愿和祝福赠送给其他同学各一张,全班共互赠了1980张,设全班有x名同学,那么根据题意列出的方程是( )A、x(x+1)=1980 B、x(x-1)=1980 C、x(x+1)=1980×2 D、x(x-1)=1980×219. 在同一平面直角坐标系中,函数y=ax+a和y=-ax2+2x+2(a是常数,且a≠0)的图象可能是( )A、
A、 B、 C、 D、18. 九年级(1)班的全体同学,在新年来临之际,在贺卡上写上自己的心愿和祝福赠送给其他同学各一张,全班共互赠了1980张,设全班有x名同学,那么根据题意列出的方程是( )A、x(x+1)=1980 B、x(x-1)=1980 C、x(x+1)=1980×2 D、x(x-1)=1980×219. 在同一平面直角坐标系中,函数y=ax+a和y=-ax2+2x+2(a是常数,且a≠0)的图象可能是( )A、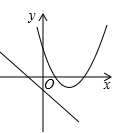 B、
B、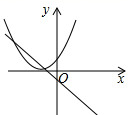 C、
C、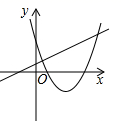 D、
D、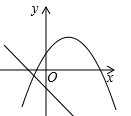 20. 二次函数 的图象如图所示,则下
20. 二次函数 的图象如图所示,则下列结论:① ,② ,③ ,④ ,⑤ 中正确的是( )
 A、②④⑤ B、①②④ C、①③④ D、①③④⑤
A、②④⑤ B、①②④ C、①③④ D、①③④⑤三、解答题
-
21. 解方程:(1)、x2-3x-4=0;(2)、x(x+3)-(2x+6)=0.22. 先化简(1+ )÷ ,再从1、﹣1、0、2中选择一个合适的数代入并求值.23. 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
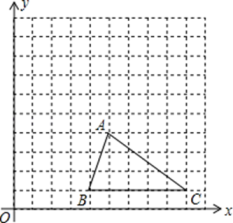
⑴将△ABC向上平移3个单位长度,画出平移后的△A1B1C1;
⑵写出A1、C1的坐标;
⑶将△A1B1C1绕B1逆时针旋转90°,画出旋转后的△A2B1C2 .
24. 如图,抛物线y=+bx+c经过坐标原点,并与x轴交于点A(2,0). (1)、求此抛物线的解析式;(2)、写出顶点坐标及对称轴;(3)、若抛物线上有一点B,且=8,求点B的坐标.25. 在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)、求此抛物线的解析式;(2)、写出顶点坐标及对称轴;(3)、若抛物线上有一点B,且=8,求点B的坐标.25. 在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
 (1)、该班共有名学生;(2)、补全条形统计图;(3)、在扇形统计图中,“乒乓球”部分所对应的圆心角度数为°.(4)、若全校有1830名学生,请计算出“其他”部分的学生人数.26. 已知:正方形 中, , 绕点A顺时针旋转,它的两边分别交 (或它们的延长线)于点 .
(1)、该班共有名学生;(2)、补全条形统计图;(3)、在扇形统计图中,“乒乓球”部分所对应的圆心角度数为°.(4)、若全校有1830名学生,请计算出“其他”部分的学生人数.26. 已知:正方形 中, , 绕点A顺时针旋转,它的两边分别交 (或它们的延长线)于点 .当 绕点A旋转到 时(如图1),易证 .
 (1)、当 绕点A旋转到 时(如图2),线段 和 之间有怎样的数量关系?写出猜想,并加以证明.(2)、当 绕点A旋转到如图3的位置时,线段 和 之间又有怎样的数量关系?请直接写出你的猜想.27. 某衬衣店将进价为30元的一种衬衣以40元售出,平均每月能售出600件,调查表明:这种衬衣售价每上涨1元,其销售量将减少10件.(1)、求出月销售利润y(元)与售价x(元/件)之间的函数关系式;(2)、衬衣店想在月销售量不少于300件的情况下,使月销售利润达到10000元,则售价应定为多少?(3)、当销售价定为多少元时会获得最大利润?求出最大利润.28. 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB).
(1)、当 绕点A旋转到 时(如图2),线段 和 之间有怎样的数量关系?写出猜想,并加以证明.(2)、当 绕点A旋转到如图3的位置时,线段 和 之间又有怎样的数量关系?请直接写出你的猜想.27. 某衬衣店将进价为30元的一种衬衣以40元售出,平均每月能售出600件,调查表明:这种衬衣售价每上涨1元,其销售量将减少10件.(1)、求出月销售利润y(元)与售价x(元/件)之间的函数关系式;(2)、衬衣店想在月销售量不少于300件的情况下,使月销售利润达到10000元,则售价应定为多少?(3)、当销售价定为多少元时会获得最大利润?求出最大利润.28. 如图,在平面直角坐标系中,正方形ABCD的顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA、OB的长分别是一元二次方程x2﹣7x+12=0的两个根(OA>OB). (1)、求点D的坐标.(2)、求直线BC的解析式.(3)、在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.
(1)、求点D的坐标.(2)、求直线BC的解析式.(3)、在直线BC上是否存在点P,使△PCD为等腰三角形?若存在,请直接写出点P的坐标;若不存在,说明理由.