广东省云浮市新兴县2021—2022学年九年级上学期期中质量监测数学试卷

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四幅图片上呈现的是垃圾类型及标识图案，其中标识图案不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 方程 $x^{2} - 3 x - 1 = 0$ 的二次项系数和一次项系数分别为（）

A、1和3 B、1和-3 C、0和-1 D、-3和-1

查看试题解析
3. 点A(﹣3，a)与点B(3，4)关于原点对称，则a的值为（　　）

A、﹣3 B、﹣4 C、3 D、4

查看试题解析
4. 一元二次方程x²﹣4x+4＝0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、没有实数根

查看试题解析
5. 若点(2，5)，(4，5)在抛物线y＝ax²＋bx＋c上，则它的对称轴是（）

A、x＝2 B、x＝3 C、x＝4 D、x＝5

查看试题解析
6. 用配方法解方程x²﹣10x﹣1＝0时，变形正确的是（　　）

A、（x﹣5）²＝24 B、（x﹣5）²＝26 C、（x+5）²＝24 D、（x+5）²＝26

查看试题解析
7. 将抛物线 $y = - 2 x^{2} + 1$ 绕原点 $O$ 旋转180°，则旋转后抛物线的解析式为（）

A、 $y = 2 x^{2}$ B、 $y = 2 x^{2} + 1$ C、 $y = - 2 x^{2} - 1$ D、 $y = 2 x^{2} - 1$

查看试题解析
8. 将抛物线 $y = 2 x^{2} - 2$ 先向右平移1个单位长度，再向下平移3个单位长度后，得到抛物线的解析式是（）

A、 $y = 2 {(x + 1)}^{2} + 1$ B、 $y = 2 {(x + 1)}^{2} - 5$ C、 $y = 2 {(x - 1)}^{2} - 5$ D、 $y = 2 {(x - 1)}^{2} + 1$

查看试题解析
9. 给出一种运算：对于函数 $y = x^{n}$ ，规定 $y^{'} = n x^{n - 1}$ ．例如：若函数 $y = x^{4}$ ，则有 $y^{'} = 4 x^{3}$ ．已知函数 $y = x^{3}$ ，那么方程 $y^{'} = 18$ 的解是（）

A、 $x_{1} = \sqrt{6}$ ， $x_{2} = - \sqrt{6}$ B、 $x_{1} = 6$ ， $x_{2} = - 6$ C、 $x_{1} = 3$ ， $x_{2} = - 3$ D、 $x_{1} = 3 \sqrt{2}$ ， $x_{2} = - 3 \sqrt{2}$

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c$ 的图象经过点 $A (- 3 ， 0)$ ，其对称轴为直线 $x = - 1$ ，有下列结论：① $a b c < 0$ ；② $a + b + c < 0$ ；③ $2 a - b = 0$ ；④ $4 a c - b^{2} > 0$ ；⑤若 $P (- 5 ， y_{1})$ ， $Q (m ， y_{2})$ 是抛物线上两点，且 $y_{1} > y_{2}$ ，则实数 $m$ 的取值范围是 $- 5 < m < 3$ ．其中正确结论是（）

A、①③④ B、②④⑤ C、①③⑤ D、①③④⑤

查看试题解析

二、填空题

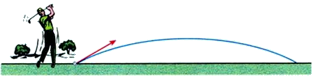
11. 已知x＝1是方程x²＋x＋c＝0的解，则c的值是．

查看试题解析
12. 抛物线 $y = 2 x^{2} - b x + 3$ 的对称轴是直线 $x = 2$ ，则它的顶点坐标为

查看试题解析
13. 如图，若被击打的小球飞行高度 $h$ （单位： $m$ ）与飞行时间 $t$ （单位： $s$ ）之间具有的关系为 $h = 20 t - 5 t^{2}$ ，则小球从飞出到落地所用的时间为 $s$ .

查看试题解析
14. 如图，将△ABC绕点A逆时针旋转100°，得到△ADE.若点D在线段BC的延长线上，则 $∠ B$ 的大小为.

查看试题解析
15. 已知点（－1，y₁），（2，y₂）在抛物线y＝x²－2x＋c上，则y₁ ， y₂的大小关系是y₁y₂（填“>”，“<”或“＝”）．

查看试题解析
16. 关于 $x$ 的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，下列命题是真命题的是．（填序号）
①若 $a + 2 b + 4 c = 0$ ，则方程 $a x^{2} + b x + c = 0$ 必有实数根；
②若 $b = 3 a + 2$ ， $c = 2 a + 2$ ，则方程 $a x^{2} + b x + c = 0$ 必有两个不相等的实根；
③若 $c$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $a c + b + 1 = 0$ 成立；
④若 $t$ 是一元二次方程 $a x^{2} + b x + c = 0$ 的根，则 $b^{2} - 4 a c = {(2 a t + b)}^{2}$ ．

查看试题解析

三、解答题

17. 用公式法解方程： $5 x^{2} = 7 - 2 x$ ．

查看试题解析
18. 用适当的方法解下列方程： $x (x - 3) - 5 (3 - x) = 0$ ．

查看试题解析
19. 如图， $△ A B C$ 三个顶点的坐标分别为 $A (2 ， 4)$ ， $B (1 ， 1)$ ， $C (4 ， 3)$

(1)、请画出 $△ A B C$ 关于原点对称的 $△ A_{1} B_{1} C_{1}$ ；

(2)、请图出 $△ A B C$ 绕点 $B$ 逆时针旋转90°后的 $△ A_{2} B C_{2}$ ．

查看试题解析
20. 在 $△ A B C$ 中， $∠ B + ∠ A C B = 30 °$ ， $A B = 4$ ， $△ A B C$ 逆时针旋转一定角度后与 $△ A D E$ 重合，且点 $C$ 恰好成为 $A D$ 中点，如图．

(1)、旋转中心是点， $A E =$ ；

(2)、求直线 $B C$ 与直线 $D E$ 的夹角．

查看试题解析
21. 已知二次函数 $y = - 2 x^{2} + 8 x - 6$ ．

(1)、把它配方成 $y = a {(x - h)}^{2} + k$ 的形式，并写出它的开口方向、顶点 $M$ 的坐标；

(2)、作出函数的图象（列表描出五个关键点）．
$x$
…
0
1
2
3
4
…
$y$
…
…

查看试题解析
22. 已知：如图，在边长为4的正方形ABCD中，点F是边DC的中点，连接AF，并将线段AF绕点A顺时针旋转90°得到线段AE，连接EF，取EF的中点G，连接CG．

(1)、请根据题意补全图形；

(2)、求线段CG的长．

查看试题解析
23. 某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图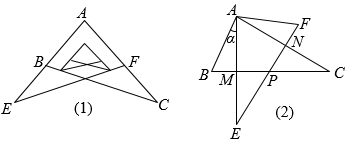

(1)、所示位置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．
求证：AM=AN；

(2)、当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．

查看试题解析
24. 某商场销售一种小商品，进货价为8元/件．当售价为10元/件时，每天的销售量为100件．在销售过程中发现：销售单价每上涨0.1元，每天的销售量就减少1件．设销售单价为x（元/件）（x≥10），每天销售利润为y（元）．

(1)、直接写出y与x的函数关系式；

(2)、若要使每天销售利润为270元，求此时的销售单价；

(3)、若每件该小商品的利润率不超过100%，且每天的进货总成本不超过800元，求该小商品每天销售利润y的取值范围．

查看试题解析
25. 在平面直角坐标系中，抛物线y＝ax²＋bx－3交x轴于点A（－1，0），B（3，0），过点B的直线y＝ $\frac{2}{3}$ x－2交抛物线于点C．

(1)、求该抛物线的函数表达式；

(2)、若点P是直线BC下方抛物线上的一个动点（P不与点B，C重合），求△PBC面积的最大值；

(3)、若点M在抛物线上，点N直线BC上．试探究：是否存在点M，N，使得OM=ON，∠MON=90°同时成立？若存在，请直接写出点N的坐标；若不存在，请说明理由．

查看试题解析

$x$	…	0	1	2	3	4	…
$y$	…						…