广东省阳江市阳东区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是一元二次方程的有（）
① $5 x^{2} = x$ ；② ${(x^{2} - 3)}^{2} - 6 = 0$ ；③ $3 x^{2} = 1$ ；④ $7 x (x - 2) = 7 x^{2}$ ；⑤ $6 x^{2} + \frac{1}{x} - 2 = 0$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 若y=（m﹣1） $x^{m^{2} + m}$ 是关于x的二次函数，则m的值为（）

A、﹣2 B、﹣2或1 C、1 D、不存在

查看试题解析
3. 以下函数的图象的顶点坐标为 $(2 ， 0)$ 的是（）

A、 $y = 3 x^{2} + 2$ B、 $y = 3 x^{2} - 2$ C、 $y = 3 {(x - 2)}^{2}$ D、 $y = 3 {(x + 2)}^{2}$

查看试题解析
4. 已知点 $(2 ， - 4)$ 在抛物线 $y = m x^{2} - 2 m x + n$ 上，则下列点中，一定也在该抛物线上的是点（）

A、 $(0 ， - 4)$ B、 $(0 ， 4)$ C、 $(3 ， - 4)$ D、 $(- 2 ， 4)$

查看试题解析
5. 二次函数y=x²的图象平移后经过点（2，0），则下列平移方法正确的是（　　）

A、向左平移2个单位，向下平移2个单位 B、向左平移1个单位，向上平移2个单位 C、向右平移1个单位，向下平移1个单位 D、向右平移2个单位，向上平移1个单位

查看试题解析
6. 一元二次方程 $x (x + 1) - x = 1$ 的根是（）

A、 $x_{1} = x_{2} = - 1$ B、 $x_{1} = x_{2} = 1$ C、 $x_{1} = 1$ ， $x_{2} = - 1$ D、 $x_{1} = x_{2} = 0$

查看试题解析
7. 无论m取何实数，关于x的二次函数 $y = a (x - m)^{2} + m^{2} + 1 (a \neq 0)$ 的图象的顶点都（）

A、在抛物线 $y = x^{2} + 1$ 上 B、在抛物线 $y = - x^{2} - 1$ 上 C、在抛物线 $y = - x^{2} + 1$ 上 D、在抛物线 $y = - x^{3} + x$ 上

查看试题解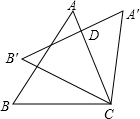析
8. 如图，把 $△ A B C$ 绕点 $C$ 顺时针旋转 $35 °$ ，得到 $△ A^{'} B^{'} C^{'}$ ， $A^{'} B^{'}$ 交 $A C$ 于点 $D$ ，若 $∠ A^{'} C B = 105 °$ ，则 $∠ A C B^{'}$ 度数为（）

A、45° B、30° C、35° D、70°

查看试题解析
9. 已知点 $A (a - 1 ， - 1)$ 与点 $B (2 ， b + 3)$ 关于原点对称，则抛物线 $y = a x^{2} + b x + 3$ 的顶点坐标是（）

A、(1，4) B、(-1，4) C、(1，-4) D、(-1，-4)

查看试题解析
10. 二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，有如下结论：① $a b c > 0$ ；② $2 a + b = 0$ ；③ $3 b - 2 c < 0$ ；④ $a m^{2} + b m \geq a + b$ （m为实数）.其中正确结论的个数是（）

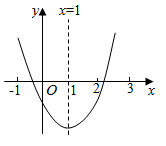A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 一元二次方程x²﹣7x＝0的较大根为．

查看试题解析
12. 若关于x的一元二次方程 $x^{2} + 2 x - k = 0$ 无实数根，则k的取值范围是.

查看试题解析
13. 在平面直角坐标系中，点 $A (x^{2} ， - 3)$ 与点 $B (2 x ， 3)$ 关于原点对称，则点A的坐标为．

查看试题解析
14. 二次函数 $y = - \frac{1}{2} x^{2} - 2$ 的图象的对称轴为．

查看试题解析
15. 已知二次函数y＝2x²+bx+4顶点在x轴上，则b＝．

查看试题解析
16. 已知二次函数y＝mx²+(m²﹣3)x+1，当x＝﹣1时，y取得最大值，则m＝．

查看试题解析
17. 如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2，将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是

查看试题解析

三、解答题

18. 解方程： $3 {(x - 5)}^{2} = 4 (5 - x)$ ．

查看试题解析
19. 已知二次函数 $y = a x^{2} + b x + c$ 中，函数值y与自变量x的部分对应值如表，求这个二次函数的解析式．
x
…
-1
0
1
2
4
…
y
…
10
1
-2
1
25
…

查看试题解析
20. 直角坐标系第二象限内的点P（x²+2x，3）与另一点Q（x+2，y）关于原点对称，试求x+2y的值．

查看试题解析
21. 已知关于x的一元二次方程 $x^{2} - (a - 3) x - a = 0$ ．

(1)、求证：无论a取何值，该方程总有两个不相等的实数根；

(2)、若该方程两根的平方和为21，求a的值．

查看试题解析
22. 如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度为11米）围成中间隔有一道篱笆的长方形花圃．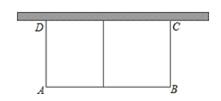

(1)、如果要围成面积为45平方米的花圃，那么AD的长为多少米？

(2)、能否围成面积为60平方米的花圃？若能，请求出AD的长；若不能，请说明理由．

查看试题解析
23. 方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后， $△ A B C$ 的顶点均在格点上．

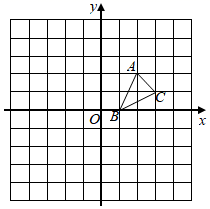(1)、画出 $△ A B C$ 绕 $B$ 点顺时针旋转 $90 °$ 后的 $△ A_{1} B_{1} C_{1}$ ，并写出 $A_{1}$ 的坐标；

(2)、画出 $△ A B C$ 关于原点 $O$ 对称的 $△ A_{2} B_{2} C_{2}$ ．

查看试题解析
24. 某超市销售一款洗手液，这款洗手液成本价为每瓶16元，当销售单价定为每瓶20元时，每天可售出60瓶．市场调查反应：销售单价每上涨1元，则每天少售出5瓶．若设这款洗手液的销售单价上涨x元，每天的销售量利润为y元．

(1)、每天的销售量为瓶，每瓶洗手液的利润是元；（用含x的代数式表示）

(2)、若这款洗手液的日销售利润y达到300元，则销售单价应上涨多少元？

(3)、当销售单价上涨多少元时，这款洗手液每天的销售利润y最大，最大利润为多少元？

查看试题解析
25. 受新型冠状病毒影响，学生在进入学校大门时都要配合监测体温．某学校上学高峰期学生到达学校的人数（包括校门口等待检测的学生和已经检测体温入校的学生）y（人）随时间x（分钟）的变化情况如图所示，已知前12分钟，y可看作是x的二次函数，并在12分钟时，学生到达学校人数y达到最大值为720人，回答下列问题：

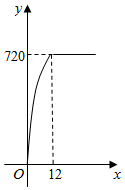(1)、当0≤x≤12时，求y与x之间的函数解析式；

(2)、已知学校门口有体温检测岗位3个，每个岗位的工作人员每分钟能检测10人，求学校门口等待接受体温测量的队伍最多时有多少人；

(3)、在（2）的条件下，从测温开始到所有学生测温结束，当学校门口等待接受体温测量的人数随时间的增加而减少时，直接写出对应的x的取值范围．

查看试题解析

x	…	-1	0	1	2	4	…
y	…	10	1	-2	1	25	…