广东省江门市蓬江区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 下面结论正确的是（）

A、互为相反数的两个数的商为-1 B、在数轴上与表示数4的点相距3个单位长度的点对应的数是7或1 C、当|x|=-x，则x＜0 D、带有负号的数一定是负数

查看试题解析
2. 如果 $| m + n | = | m | + | n |$ ，则（）

A、 $m 、 n$ 都为正数 B、 $m 、 n$ 异号 C、 $m 、 n$ 为任意有理数 D、 $m 、 n$ 同号或 $m 、 n$ 中至少一个为零

查看试题解析
3. 如图是雷达探测到的6个目标，若目标B用(30，60°)表示，目标D用(50，210°)表示，则表示为(40，120°)的是（）

A、目标A B、目标C C、目标E D、目标F

查看试题解析
4. 在解方程组 ${\begin{array}{l} a x + 5 y = 10 \\ 4 x - b y = - 4 \end{array}$ 时，由于粗心，甲看错了方程组中的 $a$ ，得到的解为 ${\begin{array}{l} x = - 3 \\ y = - 1 \end{array}$ ，乙看错了方程组中的b，得到的解为 ${\begin{array}{l} x = 5 \\ y = 4 \end{array}$ ．则原方程组的解（）

A、 ${\begin{array}{l} x = - 2 \\ y = 8 \end{array}$ B、 ${\begin{array}{l} x = 15 \\ y = 8 \end{array}$ C、 ${\begin{array}{l} x = - 2 \\ y = 6 \end{array}$ D、 ${\begin{array}{l} x = - 5 \\ y = 8 \end{array}$

查看试题解析
5. 利用一副三角板上已知度数的角，不能画出的角是（）

A、15° B、100° C、165° D、135°

查看试题解析
6. 中国讲究五谷丰登，六畜兴旺，如图2是一个正方体展开图，图中的六个正方形内分别标有六畜：“猪”、“牛”、“羊”、“马”、“鸡”、“狗”.将其围成一个正方体后，则与“牛”相对的是（）

A、羊 B、马 C、鸡 D、狗

查看试题解析
7. 一项工程，甲单独做a小时完成，乙单独做b小时完成，甲、乙两人一起完成这项工程所需的时间为（）

A、 $\frac{a b}{a + b}$ 小时 B、 $\frac{a + b}{a b}$ 小时 C、 $a + b$ 小时 D、 $\frac{1}{a + b}$ 小时

查看试题解析
8. 如图，已知AB是圆柱底面直径，BC是圆柱的高在圆柱的侧面上，过点A、C嵌有一圈路径最短的金属丝．现将圆柱侧面沿BC剪开，所得的侧面展开图是（）

A、 B、 C、 D、

查看试题解析
9. 如图所示，将形状和大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为a₁ ，第2幅图形中“●”的个数为a₂ ，第3幅图形中“●”的个数为a₃ ， …，以此类推，则 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + ⋯ + \frac{1}{a_{10}}$ 的值为（）

A、 $\frac{11}{24}$ B、 $\frac{11}{48}$ C、 $\frac{125}{223}$ D、 $\frac{175}{264}$

查看试题解析
10. 已知抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=2，与x轴的一个交点坐标为（4，0），其部分图象如图所示，下列结论：
①抛物线过原点；
②4a+b+c=0；
③a﹣b+c＜0；
④抛物线的顶点坐标为（2，b）；
⑤当x＜2时，y随x增大而增大．
其中结论正确的是（）

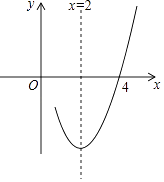A、①②③ B、③④⑤ C、①②④ D、①④⑤

查看试题解析

二、填空题

11. 若直角三角形的两边长分别为1和2，则斜边上的中线长为.

查看试题解析
12. $5^{8} - 1$ 能被20至30之间的两个整数整除，那么这两个整数是．

查看试题解析
13. 如图，把 $△ A B C$ 的一角折叠，若 $∠ 1 + ∠ 2 = 13 0^{∘}$ ，则 $∠ A$ 的度数为 .

查看试题解析
14. 分解因式；．x³﹣3x²﹣6x+8= ．

查看试题解析
15. △ABC中，AB=5，AC=3，AD是△ABC的中线，设AD长为m，则m的取值范围是．

查看试题解析
16. 在日常生活中如取款、上网等都需要密码，有一种用“因式分解法”产生的密码，方便记忆，原理是对于多项x⁴﹣y⁴ ，因式分解的结果是（x﹣y）（x+y）（x²+y²），若取x＝9，y＝9时，则各个因式的值是：（x+y）＝18，（x﹣y）＝0，（x²+y²）＝162，于是就可以把“180162”作为一个六位数的密码，对于多项式9x³﹣xy² ，取x＝10，y＝10时，用上述方法产生的密码是（写出一个即可）.

查看试题解析
17. 如图，在平面直角坐标系中，一动点沿箭头所示的方向，每次移动一个单位长度，依次得到点 $P_{1} (0 ， 1)$ ， $P_{2} (1 ， 1)$ ， $P_{3} (1 ， 0)$ ， $P_{4} (1 ， - 1)$ ， $P_{5} (2 ， - 1)$ ，…，则 $P_{2021}$ 的坐标是.

查看试题解析

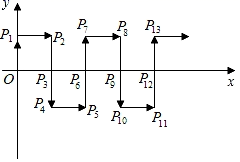
三、解答题

18. 已知实数a，b，c在数轴上的位置如图所示，化简代数式： $\sqrt{a^{2}} - | a + c | + \sqrt{{(c - b)}^{2}} - | - b |$

查看试题解析
19. 当m为何值时，关于x的方程 $\frac{x + 1}{x - 2}$ ﹣ $\frac{x}{x + 3}$ ＝ $\frac{x + m}{(x - 2) (x + 3)}$ 的解为负数？

查看试题解析

20. 为积极响应“弘扬传统文化”的号召，某学校倡导全校1200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根调查结果绘制成的统计图（部分）如图所示．

大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表

一周诗词诵背数量	3首	4首	5首	6首	7首	8首
人数	10	10	15	40	25	20

请根据调查的信息分析：

(1)、活动启动之初学生“一周诗词诵背数量”的中位数为；

(2)、估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；

(3)、选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．

查看试题解析

21. 如图，AD＝DE＝EC，F是BC中点，G是FC中点，如果三角形ABC的面积是24平方厘米，则阴影部分是多少平方厘米？

查看试题解析
22. 如图，在平面直角坐标系xOy中，A、B分别是x轴正半轴、y轴正半轴上的一点，以AB为斜边作等腰直角三角形，直角顶点C（a，b）在第二象限．

(1)、探究a、b之间的数量关系并证明．

(2)、若BO平分∠ABC，AC与OB交于点D，且A（2，0），B（0，2 $\sqrt{2}$ +2），求点D的坐标．

查看试题解析
23. 我们已知学过完全平方公式 $a^{2} \pm 2 a b + b^{2} = (a \pm b)^{2}$ ，知道所有的非负数都可以看作一个数的平方，如 $2 = (\sqrt{2})^{2} ， 3 = (\sqrt{3})^{2}$ 等，那么，我们可以利用这种思想方法和完全平方公式来计算下面的题：
例：求 $3 - 2 \sqrt{2}$ 的算术平方根．
解： $3 - 2 \sqrt{2} = 2 - 2 \sqrt{2} + 1 = (\sqrt{2})^{2} - 2 \sqrt{2} + 1^{2}$ = $(\sqrt{2} - 1)^{2}$ ，所以 $3 - 2 \sqrt{2}$ 的算术平方根是 $\sqrt{2} - 1$ ．你看明白了吗？请根据上面的方法解答下列问题：

(1)、填空： $\sqrt{3 + 2 \sqrt{2}}$ =；
$\sqrt{10 + 8 \sqrt{3 + 2 \sqrt{2}}}$ =；

(2)、化简： $\sqrt{3 - 2 \sqrt{2}}$ + $\sqrt{5 - 2 \sqrt{6}}$ + $\sqrt{7 - 2 \sqrt{12}}$ + $\sqrt{9 - 2 \sqrt{20}}$ + $\sqrt{11 - 2 \sqrt{30}}$ ．

查看试题解析
24. 先阅读短文，然后回答短文后面所给出的问题：
对于三个数a、b、c的平均数，最小的数都可以给出符号来表示，我们规定M{a，b，c}表示这三个数的平均数，min{a，b，c}表示这三个数中的最小的数，max{a，b，c}表示这三个数中最大的数．例如：M{﹣1，2，3}＝ $\frac{- 1 + 2 + 3}{3} = \frac{4}{3}$ ， min{﹣1，2，3}＝﹣1，max{﹣1，2，3}＝3；M{﹣1，2，a}＝ $\frac{- 1 + 2 + a}{3}$ ＝ $\frac{a + 1}{3}$ ， min{﹣1，2，a}＝ ${\begin{array}{l} a (a \leq - 1) \\ - 1 (a > - 1) \end{array}$ ．

(1)、请填空：min{﹣1，3，0}＝；若x＜0，则max{2，x²+2，x+1}＝；

(2)、若min{2，2x+2，4﹣2x}＝M{x﹣1，5﹣4x，3x+2}，求x的取值范围．

(3)、若M{2，x+1，2x}＝min{2，x+1，2x}，求x的值．

查看试题解析
25. 已知： $▱$ ABCD的对角线交点为O，点E、F分别在边AB、CD上，分别沿DE、BF折叠四边形ABCD，A、C两点恰好都落在O点处，且四边形DEBF为菱形（如图）．

(1)、求证：四边形ABCD是矩形；

(2)、在四边形ABCD中，求 $\frac{A B}{B C}$ 的值．

查看试题解析
26. 请用两种方法证明；△ABC中，若∠C＝90°，则a²+b²＝c² ．

查看试题解析
27. 如图1，抛物线y＝- $\frac{\sqrt{3}}{3}$ x²+ $\frac{2 \sqrt{3}}{3}$ x+ $\sqrt{3}$ 与x轴交于A、B两点(点A在点B的左侧)，交y轴于点C．将直线AC以点A为旋转中心，顺时针旋转90°，交y轴于点D，交拋物线于另一点E．

(1)、求直线AE的解析式；

(2)、点F是第一象限内抛物线上一点，当△FAD的面积最大时，求出此时点F的坐标；

(3)、如图2，将△ACD沿射线AE方向以每秒 $\frac{2 \sqrt{3}}{3}$ 个单位的速度平移，记平移后的△ACD为△A′C′D′，平移时间为t秒，当△AC′E为等腰三角形时，求t的值．

查看试题解析