广东省佛山市顺德区2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 在 ▱ ABCD中，添加以下哪个条件能判断其为菱形（）

A、AB⊥BC B、BC⊥CD C、CD⊥AC D、AC⊥BD

查看试题解析
2. 方程x²=x的根是（）

A、x=1 B、x=0 C、x₁=1，x₂=0 D、x₁=1，x₂=－1

查看试题解析
3. 如图，菱形ABCD的对角线AC、BD的长分别为6和8，O为AC、BD的交点，H为AD上的中点，则OH的长度为（）

A、3 B、4 C、2.5 D、5

查看试题解析
4. 已知粉笔盒里有8支红色粉笔和n支白色粉笔，每支粉笔除颜色外均相同，现从中任取一支粉笔，取出红色粉笔的概率是 $\frac{2}{5}$ ，则n的值是（）

A、10 B、12 C、13 D、14

查看试题解析
5. 小明语数英的科目成绩的排序为语文>数学>英语．到家后，小明妈妈从小明书包依次抽2张试卷，若第二次抽到的试卷比第一次抽到的试卷成绩高的话，则小明可以获得奖励．请问小明获得奖励的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{3}$ D、 $\frac{1}{6}$

查看试题解析
6. 如图，矩形ABCD中，AC交BD于点O，且AB=24，BC=10，将AC绕点C顺时针旋转90°至CE．连接AE，且F、G分别为AE、EC的中点，则四边形OFGC的面积是（）

A、100 B、144 C、169 D、225

查看试题解析
7. 如图，已知矩形纸张长比宽长2cm，小明将其折成飞机，假设纸张的宽为xcm，在第一步结束后，纸张面积为20cm² ，则下列方程正确的是（）

A、 $\frac{3}{4} x^{2}$ +2x=20 B、x²+ $\frac{7}{4} x$ =20 C、 $\frac{7}{8} x^{2}$ +2x=20 D、x² +2x=20

查看试题解析
8. 已知实数a，b满足a≠b，且a²－4a＝b²－4b＝2，则a²＋b²的值为（）

A、16 B、20 C、25 D、30

查看试题解析
9. 如图，正方形ABCO和正方形DEFO的顶点A、E、O在同一直线上，且EF= $\sqrt{2}$ ， AB=3，给出下列结论：①∠COD=45°；②AE=3+ $\sqrt{2}$ ；③CF=AD= $\sqrt{17}$ ；④S_△COF+S_△EOF= $\frac{5}{2}$ ．期中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、多选题

10. 关于x的一元二次方程(k－1)x² +4x+k－1=0有两个相等的实数根，则k的值为（）

A、1 B、0 C、3 D、－3

查看试题解析

三、填空题

11. 一元二次方程（x+1）（x-2）=0的解为.

查看试题解析
12. 已知菱形ABCD中，AB=4，∠ABC＝120°，则AC＝．

查看试题解析
13. 如图，正方形ABCD中，BD为对角线，且BE为∠ABD的角平分线，并交CD延长线于点E，则∠E＝°．

查看试题解析
14. 八卦是中国文化的基本哲学概念，如图是八卦模型图，其制作要样板为图中的正八边形ABCDEFGH，已知八卦模型图的周长为10cm，在模型放大3倍的样板图中AB＋BC＋CD＋DE＝cm．

查看试题解析
15. 若 $\frac{3 x + y}{x + y} = 2$ ，则 $\frac{y}{x}$ ＝．

查看试题解析
16. 若m、n是一元二次方程x²－2021x＋1＝0的两个实数根，则 $\frac{1}{m} +$ $\frac{1}{n}$ 的值为．

查看试题解析
17. 在直角墙角FOE中有张硬纸片正方形ABCD靠墙边滑动，如图所示，AD=2，A点沿墙往下滑动到O点的过程中，正方形的中心点M到O的最小值是．

查看试题解析

四、解答题

18. 按指定方法，解下列方程：

(1)、x²－8x＋12＝0(配方法)；

(2)、x²＋3x－1＝0(公式法)．

查看试题解析
19. 已知四边形ABCD是平行四边形，

(1)、作∠ADC的角平分线，与AB交于点E (用尺规作图，保留作图痕迹，不要求写作法)；

(2)、若点E恰好与点B重合，求证：四边形ABCD为菱形．

查看试题解析
20. 如图所示，有一面积为150m²的的长方形养鸡场，鸡场边靠墙(墙长18米)，另三边用竹篱笆围成．如果竹篱笆的长为35m，求鸡场长和宽各是多少?

查看试题解析
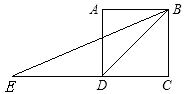
21. 网上购物已经成为人们常用的一种购物方式，售后评价特别引人关注，消费者在网店购买某种商品后，结果有“好评”、“中评”、“差评”三种评价，假设这三种评价是等可能的．小明对一家网店销售某种商品显示的评价信息进行了统计，并列出了两幅不完整的统计图，利用图中所提供的信息解决以下问题：

(1)、请将图1补充完整；

(2)、图2中“差评”所占的百分比是；

(3)、若甲、乙两名消费者在该网店购买了同一商品，请你用表格或画树状图的方法帮助店主求一下两人中至少有一个给“好评”的概率．

查看试题解析
22. 如图，在矩形ABCD中，AC交BD于点E，且四边形AEBF为菱形，已知BD=2BC=8，求FD与四边形ADEF的面积．

查看试题解析
23. 山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：

(1)、每千克核桃应降价多少元？

(2)、在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？

查看试题解析
24. 如图，在四边形ABCD中，AD∥BC，AB＝8cm，AD＝12cm，BC=18cm，点P从点A出发，以1cm/s的速度向点D运动，点Q从点C出发，以2cm/s的速度向点B运动．规定其中一个动点到达端点时，另一个动点也随之停止运动．设点P的运动时间为ts，

(1)、CD边的长度为cm，t的取值范围为．

(2)、从运动开始，当t取何值时，PQ∥CD？

(3)、从运动开始，当t取何值时，PQ＝CD？

(4)、在整个运动过程中是否存在t值，使得四边形PQCD是菱形？若存在，请求出t值，请说明理由．

查看试题解析
25. 已知正方形ABCD中，AB=3，且E为CD上的一动点，以AE为边作正方形AGFE，如下图1所示，连接BE、GD

(1)、求证：BE=GD．

(2)、如图2，延长GD、BE交于点Q，求证：BE⊥GD．

(3)、若∠QED=60°，则DE的值是多少?

查看试题解析