广东省佛山市2021-2022学年九年级上学期期中数学试题

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示的几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
2. 某反比例函数的图象经过点 $(- 2 ， 3)$ ，则该图象一定不经过点（）

A、 $(1 ， 6)$ B、 $(- 1 ， 6)$ C、 $(2 ， - 3)$ D、 $(3 ， - 2)$

查看试题解析
3. 从一个不透明的口袋中随机摸出一球，再放回袋中，不断重复上述过程，一共摸了150次，其中有50次摸到黑球，已知口袋中仅有黑球10个和白球若干个，这些球除颜色外，其他都一样，由此估计口袋中白球的个数约为（）

A、10 B、15 C、20 D、30

查看试题解析
4. 如图，四边形 $A B C D$ 为菱形，A ， B两点的坐标分别是 $(3 ， 0) ， (0 ， \sqrt{3})$ ，点C ， D在坐标轴上，则菱形 $A B C D$ 的周长等于（）

A、 $8 \sqrt{3}$ B、 $4 \sqrt{3}$ C、 $2 \sqrt{3}$ D、 $4 \sqrt{6}$

查看试题解析
5. 用配方法解一元二次方程x²+8x+7＝0，则方程可化为（）

A、（x+4）²＝23 B、（x+4）²＝9 C、（x﹣4）²＝23 D、（x﹣4）²＝9

查看试题解析
6. 如图，已知 $∠ D A B = ∠ E A C$ ，添加下列一个条件，不能使 $△ A D E$ ∽ $△ A B C$ 的是（）

A、 $\frac{A D}{A B} = \frac{D E}{B C}$ B、 $∠ B = ∠ D$ C、 $\frac{A D}{A B} = \frac{A E}{A C}$ D、 $∠ E = ∠ C$

查看试题解析
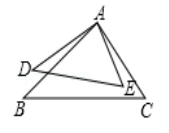7. 函数 $y = a x$ 与 $y = \frac{b}{x} (a b \neq 0)$ 的图象的两个交点的坐标分别为 $(3 ， m)$ ， $(n ， - 2)$ ，则 $m$ ， $n$ 的值分别是（）

A、2，﹣3 B、﹣2，﹣3 C、﹣2，3 D、2，3

查看试题解析
8. 在同一平面直角坐标系中，函数 $y = m x + n$ 与 $y = \frac{m n}{x} (m n \neq 0)$ 的图象可能是（）．

A、 B、 C、 D、

查看试题解析
9. 如图，AB和CD表示两根直立于地面的柱子，AC和BD表示起固定作用的两根钢筋，AC与BD相交于点M，已知AB=8m，CD=12m，则点M离地面的高度MH为（）

A、4 m B、 $\frac{24}{5}$ m C、5m D、 $\frac{16}{3}$ m

查看试题解析
10. 如图，正方形ABCD的边长是3，BP＝CQ，连接AQ，DP交于点O，并分别与边CD，BC交于点F，E，连接AE，下列结论：①AQ⊥DP；②OA²＝OE·OP；③S_△AOD＝S_四边形OECF；④当BP＝1时，OE＝ $\frac{39}{20}$ ．其中正确结论的个数是（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 一元二次方程 $x^{2} - 3 x = 0$ 的根是．

查看试题解析
12. 已知 $\frac{x}{y} = \frac{5}{2}$ ，则 $\frac{x - y}{y}$ ＝.

查看试题解析
13. 在△ABC中，∠C=90°，AC=1，BC=2，则AB边上的中线CD= ．

查看试题解析
14. 为了测量旗杆的高度，某同学测得阳光下旗杆的影长为2m，同一时刻长度为1m的标杆影长为0.4m，则旗杆的高度为m．

查看试题解析
15. 若关于x的一元二次方程kx²+4x﹣1＝0有实数根，则k的取值范围是．

查看试题解析
16. 如图，点 $A (0 ， 2 \sqrt{3})$ ，点 $B (2 ， 0)$ ，点 $P$ 为线段 $A B$ 上一个动点，作 $P M ⊥ y$ 轴于点 $M$ ，作 $P N ⊥ x$ 轴于点 $N$ ，连接 $M N$ ，当 $M N$ 取最小值时，则四边形 $O M P N$ 的面积为．

查看试题解析
17. 如图，菱形ABCD的顶点分别在反比例函数y＝ $\frac{k_{1}}{x}$ 和y＝ $\frac{k_{2}}{x}$ 的图象上，∠BCD＝60°，则 $\frac{k_{1}}{k_{2}}$ 的值为．

查看试题解析

三、解答题

18. 在一个不透明的盒子中装有3个小球，3个小球上分别标有数字1，2，3，这些小球除标注的数字不同之外其他都相同．

(1)、从盒子中任意摸出一个小球，恰好摸出奇数号小球的概率是；

(2)、先从盒子中随机摸出一个小球，记下标号后放回，将小球搅匀，再随机摸出一个小球，请用列表法或画树状图法求两次摸出的小球所标注数字之和为偶数的概率．

查看试题解析
19. 如图，在Rt△ABC中，∠ACB＝90°，CD为AB边上的高，CE为AB边上的中线，AD＝3，CE＝5，求CD的长．

查看试题解析
20. 如图，已知O是坐标原点，AB两点的坐标分别为（3，﹣1），（2，1）．

(1)、以点O为位似中心，在y轴的左侧将△OAB放大2倍；

(2)、分别写出A，B两点的对应点A′，B′的坐标．

查看试题解析
21. 已知关于x的一元二次方程x²+（m+1）x+m＝0．

(1)、不解方程，判断方程根的情况；

(2)、若x为方程的一个根，且满足0＜x＜3，求整数m的值．

查看试题解析
22. 如图，BD是△ABC的角平分线，过点作DE∥BC交AB于点E，DF∥AB交BC于点F．

(1)、求证：四边形BEDF是菱形；

(2)、若∠ABC＝45°，∠ACB＝30°，CD＝6，求菱形BEDF的边长．

查看试题解析
23. 某服装厂生产一批服装，2019年该类服装的出厂价是200元/件，2020年，2021年连续两年改进技术，降低成本，2021年该类服装的出厂价调整为162元/件．

(1)、这两年此类服装的出厂价下降的百分比相同，求平均下降率．

(2)、2021年某商场从该服装厂以出厂价购进若干件此类服装，以200元/件销售时，平均每天可销售20件．为了减少库存，商场决定降价销售．经调查发现，单价每降低5元，每天可多售出10件，如果每天盈利1150元，单价应降低多少元?

查看试题解析
24. 直线y＝kx+b与反比例函数 $y = \frac{8}{x}$ （x＞0）的图象分别交于点A（m，4）和点B（8，n），与坐标轴分别交于点C和点D.

(1)、求直线AB的解析式；

(2)、观察图象，当x＞0时，直接写出 $k x + b > \frac{8}{x}$ 的解集；

(3)、若点P是x轴上一动点，当△COD与△ADP相似时，求点P的坐标.

查看试题解析
25. 折叠变换是特殊的轴对称变换，我们生活中常对矩形纸片进行折叠，这其中蕴含着丰富的数学知识和思想．

(1)、如图1，矩形ABCD中，AB＝6，BC＝4，点E是DC的中点，将矩形ABCD沿BE折叠，点C落在点F的位置．
①求证：DF $∥$ BE；
②求DF的长度．

(2)、如图2，在直角坐标系中，把矩形OABC沿对角线AC所在的直线折叠，点B落在点D处，AD与y轴交于点E，OA＝2，OC＝2 $\sqrt{3}$ ，点G是直线AC上的一个动点，在坐标平面内存在点H，使得以点E，A，G，H为顶点的四边形是菱形，请直接写出点H坐标．

查看试题解析