北京市通州区2021-2022学年第一学期九年级期中数学试卷

试卷更新日期：2022-09-14 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示， $△ A B C ∽ △ D E F$ ，则 $∠ D$ 的度数为（）

A、 $35 °$ B、 $45 °$ C、 $65 °$ D、 $80 °$

查看试题解析
2. 下列各坐标表示的点中，在函数 $y = x^{3} + 1$ 的图象上的是（）

A、 $(- 1, - 2)$ B、 $(- 1, 4)$ C、 $(1, 2)$ D、 $(1, 4)$

查看试题解析
3. 如图，在 $△ A B C$ 中，点 $D$ 是 $A B$ 上一点， $D E // B C$ 交 $M C$ 于点 $E$ ， $A D = 3$ ， $B D = 2$ ，则 $A E$ 与 $E C$ 的比是（）

A、 $3 ： 2$ B、 $3 ： 5$ C、 $9 ： 16$ D、 $9 ： 4$

查看试题解析
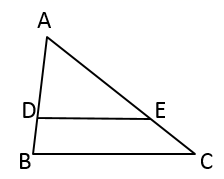4. 将二次函数 $y = - 2 x^{2}$ 的图象向上平移3个单位长度，得到新的二次函数的表达式为（）

A、 $y = - 2 x^{2} + 3$ B、 $y = - 2 x^{2} - 3$ C、 $y = - 2 (x - 3)^{2}$ D、 $y = - 2 (x + 3)^{2}$

查看试题解析
5. 如图，已知△ABC∽△BDC，其中AC＝4，CD＝2，则BC＝（）

A、2 B、 $2 \sqrt{2}$ C、 $2 \sqrt{3}$ D、4

查看试题解析
6. 已知 $(- 3 ， y_{1}) ， (1 ， y_{2})$ 是二次函数 $y = 2 x^{2} - 4 x$ 图象上的两点，那么 $y_{1} 、 y_{2}$ 的大小关系是（）

A、 $y_{1} > y_{2}$ B、 $y_{1} < y_{2}$ C、 $y_{1} = y_{2}$ D、不能确定

查看试题解析
7. 在物理课中同学们曾学过小孔成像：在较暗的屋子里，把一支点燃的蜡烛放在一块半透明的塑料薄膜前面，在它们之间数一块钻有小孔章的纸板，由于光沿直线传播，塑料薄膜上就出现了蜡烛火焰倒立的像（如图1），这种现象就是小孔成像，在图2中，如果蜡烛火焰图1根B到孔О的距离为 $4 c m$ ，火焰根的像 $B ′$ 到孔O的距离为10cm，蜡烛火焰 $A B$ 的高度为 $2 c m$ ，那么倒立的像 $A' B^{'}$ 的高度为（）

A、 $2 c m$ B、 $4 c m$ C、 $5 c m$ D、 $7 c m$

查看试题解析
8. 如图，要在二次函数 $y = x (2 - x)$ 的图象上找一点 $M (a ， b)$ ，针对b的不同取值，所找点M的个数，有下列三种说法：①如果 $b = - 3$ ，那么点M的个数为0；②如果 $b = 1$ ．那么点M的个数为1；③如果 $b = 3$ ，那么点M的个数为2．上述说法中正确的序号是（）

A、① B、② C、③ D、②③

查看试题解析

二、填空题

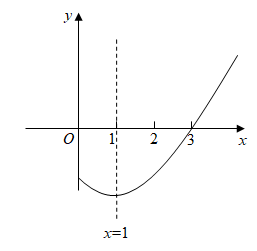
9. 如图，已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的对称轴为直线 $x = 1$ ，与x轴的一个交点是 $(3 ， 0)$ ，那么二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴的另一个交点的坐标是．

查看试题解析
10. 已知 $\frac{x}{y} = \frac{3}{5}$ ，那 $\frac{x}{x + y}$ 的值为．

查看试题解析
11. 已知点 $A (1 ， y_{1})$ 点 $B (2 ， y_{2})$ 在二次函数 $y = a x^{2} - 2 (a \neq 0)$ 的图象上，且 $y_{1} < y_{2}$ ，那么a的取值范围是．

查看试题解析
12. 已知两个相似三角形的面积之比为4：9．那么这两个相似三角形的对应边之比是．

查看试题解析
13. 在平面直角坐标系 $x O y$ 中，已知点 $P (1 ， 2)$ ，点 $Q (3 ， 2)$ ，如果二次函数 $y = a x^{2}$ 的图象与线段 $P Q$ 有交点，那么a的取值范围为．

查看试题解析
14. 二次函数 $y = a x^{2} + b x + c$ ，自变量 $x$ 与函数 $y$ 的对应值如下表．则当 $- 3 < x < 3$ 时， $y$ 满足的范围是．
$x$
…
-3
-1
1
3
…
$y$
…
-4
2
4
2
…

查看试题解析
15. 如图， $△ A B C$ 中 $∠ A C B = 90 ° ， A B = 5 ， A C = 4$ ． D是 $A C$ 的中点．在边 $A B$ 上确定点E的位置．使得 $△ A D E ∽ △ A B C$ ，那么 $A E$ 的长为．

查看试题解析
16. 如图，一座悬索桥的桥面OA与主悬钢索MN之间用垂直钢索连接，主悬钢索是抛物线形状，两端到桥面的距离OM与AN相等．小强骑自行车从桥的一端0沿直线匀速穿过桥面到达另一端A ，当他行驶18秒时和28秒时所在地方的主悬钢索的高度相同，那么他通过整个桥面OA共需秒．

查看试题解析

三、解答题

17. 已知二次函数 $y = a x^{2} + b x - 3$ 的图象经过 $A (1 ， - 4) ， B (- 1 ， 0)$ 两点．

(1)、求a和b的值；

(2)、在坐标系 $x O y$ 中画出该二次函数的图象．

查看试题解析
18. 如图，在 $△ A B C$ 中， $A C ⊥ B C$ ， D是 $B C$ 延长线上的一点，E是 $A C$ 上的一点．连接 $E D$ ．如果 $∠ A = ∠ D$ ．求证： $△ A B C ∽ △ D E C$ ．

查看试题解析
19. 在平面直角坐标系 $x O y$ 中二次函数 $y = a (x - 3)^{2} - 4$ 的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点 $C (0 ， 5)$ ．

(1)、求A、B两点的坐标；

(2)、已知点D在二次函数 $y = a (x - 3)^{2} - 4$ 的图象上，且点D和点C到x轴的距离相等，求点D的坐标．

查看试题解析
20. 如图， $B E$ 是 $△ A B C$ 的角平分线，在 $B E$ 的延长线上有一点D．满足 $C D = B C$ ．求证： $\frac{A E}{E C} = \frac{A B}{B C}$ ．

查看试题解析
21. 已知二次函数 $y = a x^{2} - 2 a x + 5 (a \neq 0)$ ，

(1)、二次函数图象的对称轴为，与y轴的交点坐标为．

(2)、当 $a = 1$ 时，如果 $P (n ， y_{1}) ， Q (n + 1 ， y_{2})$ 是该二次函数图象上的两点，且 $y_{1} > y_{2}$ ，求实数n的取值范围．

查看试题解析
22. 定义：如图①．如果点D在 $△ A B C$ 的边 $A B$ 上且满足 $∠ 1 = ∠ 2$ ．那么称点D为 $△ A B C$ 的“理根点”，如图②，在 $R t △ A B C$ 中， $∠ C = 90 ° ，$ $A B = 5 ，$ $A C = 4$ ，如果点D是 $△ A B C$ 的“理想点”，连接 $C D$ ．求 $C D$ 的长．

查看试题解析
23. 已知二次函数 $y = a x^{2} - 2 a x + a + 1 (a \neq 0)$ 图象的顶点为A，与y轴交于点B．

(1)、求顶点A的坐标；

(2)、求点B的纵坐标（用含a的代数式表示）；

(3)、横、纵坐标都是整数的点叫做整点．当二次函数 $y = a x^{2} - 2 a x + a + 1 (a \neq 0)$ 的图象与直线 $y = a + 1$ 围成的封闭区域内（不包含边界）只有2个整点时．直接写出a的取值范围．

查看试题解析
24. 如图 $△ A B C$ 中， $A B = 6 ， B C = 5 ， A C = 4$ ，点D、E分别在边 $A B 、 A C$ 上，且 $\frac{A D}{A E} = \frac{2}{3}$ ．

(1)、求证： $△ A E D ∽ △ A B C$ ，

(2)、求线段 $D E$ 长的取值范围．

查看试题解析
25. 在平面直角坐标系 $x O y$ 中，二次函数 $y = a x^{2} - 4 a x (a \neq 0)$ 的图象与x轴交于A、B两点（点A在点B的左侧）．

(1)、求A、B两点的坐标；

(2)、已知点 $P (1 ， 0) ， Q (3 ， - 2 a - 1)$ ，如果线段 $P Q$ 与二次函数 $y = a x^{2} - 4 a x (a \neq 0)$ 的图象恰有一个公共点．结合函数图象，求a的取值范围．

查看试题解析
26. 如图在 $△ A B C$ 中， $A B = A C ， ∠ B A C = 90 °$ ，过点A作 $B C$ 的垂线 $A D$ ．垂足为D，E为线段 $D C$ 上一动点（不与点C，点D重合），连接 $A E$ ．以点A为中心，将线段 $A E$ 逆时针旋转 $90 °$ 得到线段 $A F$ ，连接 $B F$ ，与线段 $A D$ 交于点G．

(1)、求证： $∠ B A E = ∠ C A F$ ；

(2)、用等式表示线段 $B G$ 与 $F G$ 的数量关系，并证明．

查看试题解析
27. 2022年北京冬奥会即将召开，敢起了人们对冰雪运动的极大热情．如图是某跳台滑雪训练场的横截面示意图，取某一位置的水平线为x轴，过跳台终点A作水平线的垂线为y轴建立平而直角坐标系，图中的抛物线 $C_{1} ： y = - \frac{1}{12} x^{2} + \frac{7}{6} x + 1$ 近似表示滑雪场地上的一座小山坡，某运动员从点О正上方3米处的A点滑出，滑出后沿一段抛物线 $C_{2} ： y = - \frac{1}{8} x^{2} + b x + c$ 运动．

(1)、当运动员运动到离A处的水平距离为4米时离水平线的高度为7米．求抛物线 $C_{2}$ 的函数表达式（不要求写出自变量工的取值范围）；

(2)、在（1）的条件下．当运动员运动的水平距离为多少米时，运动员恰好落在小山坡的B处？

查看试题解析

$x$	…	-3	-1	1	3	…
$y$	…	-4	2	4	2	…