安徽省安庆市2021-2022学年九年级上学期期中数学试题
试卷更新日期：2022-09-14 类型：期中考试
一、单选题
-
1. 二次函数y＝4（x﹣2）2﹣5的顶点坐标是（ ）A、（﹣2，5） B、（2，5） C、（﹣2，﹣5） D、（2，﹣5）2. 已知 ， 则的值等于（ ）A、 B、 C、﹣ D、﹣3. 将抛物线y=3x2向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（ ）A、y=3（x+2）2+3 B、y=3（x﹣2）2+3 C、y=3（x+2）2﹣3 D、y=3（x﹣2）2﹣34. 反比例函数图象上的两点为（x1 ， y1），（x2 ， y2），且x1＜x2＜0，则y1与y2的大小关系是（ ）A、y1＞y2 B、y1＜y2 C、y1＝y2 D、不能确定5. 如图，每个小正方形的边长均为1，则下列图中的三角形（阴影部分）与如图中的△ABC相似的是（ ）
A、
B、
C、
D、
6. 如图，在△ABC中，DE∥BC，AD：DB=1：2，则=（ ）.
A、1：2 B、1：4 C、1：8 D、1：97. 函数与在同一直角坐标系中的大致图象可能是（ ）A、
B、
C、
D、
8. 如图所示，二次函数y＝ax2+bx+c的图象与x轴的交点的横坐标分别为﹣3和1，则下列结论：①abc＜0；②b2﹣4ac＞0；③a+b+c＜0；④方程ax2+bx+c＝0的解是x1＝﹣3，x2＝1；⑤不等式ax2+bx+c＞0的解集是﹣3＜x＜1．其中正确的有几个？（ ）
A、5个 B、4个 C、3个 D、2个9. 已知三个边长分别为2、3、5的正方形如图排列，则图中阴影部分的面积为（ ）
A、2.5 B、3.25 C、3.75 D、410. 如图，在△ABC中，∠BAC＝90°，AB＝AC＝4，点D是边BC上一动点（不与B，C重合），∠ADE＝45°，DE交AC于点E，下列结论：①△ADE与△ACD一定相似；②△ABD与△DCE一定相似；③当AD＝3时，；④0＜CE≤2．其中正确的结论有几个？（ ）
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 已知反比例函数的图象位于第二、四象限，则k的取值范围是 ．12. 如图所示，已知l1∥l2∥l3 ， AB＝2，DE＝BC＝3，则EF＝ ．
13. 如图所示，一条河流的两岸互相平行，沿南岸有一排大树，每隔4米一棵，沿北岸有一排电线杆，每两根电线杆之间的距离为80米，一同学站在距南岸9米的点P处，正好北岸相邻的两根电线杆被南岸的5棵树遮挡住，那么这条河流的宽度是 米．
14. 已知，抛物线y＝mx2+2mx+n（m＞0）上有两点P（t，y1）和Q（t+3，y2）．(1)、此抛物线的对称轴是 ．(2)、若y1＞y2 ， 则t的取值范围是 ．三、解答题
-
15. 通过配方，确定抛物线y＝2x2+4x+1的顶点坐标，并直接写出y的取值范围．16. 已知抛物线与x轴交于A（﹣2，0）、B（3，0）两点，与y轴交于点C（0，3），求此抛物线的解析式．17. 如图，点D、E、F分别在△ABC的三条边上，且DE∥BC，DF∥AC．求证：△ADE∽△DBF．
18. 如图，函数的图象与函数y2＝ax+b的图象交于A、B两点，已知A点的坐标为（3，1），B点坐标为（1，n）．
(1)、求k和n的值；(2)、观察图象，比较当x＞0时，y1和y2的大小．19. 如图，在四边形ABCD中，AD∥BC，∠C＝90°，BD平分∠ABC，E是BD的中点．
(1)、求证：AE⊥BD；(2)、若AB＝4，BC＝6，求BD的长．20. 已知函数y＝ax2﹣（2a+1）x+（a﹣1）的图象与坐标轴有且只有两个交点，求a的值．21. 某小区计划建一个矩形花圃，花圃的一边利用长为a的墙，另三边用总长为79米的篱笆围成，围成的花圃是如图所示的矩形ABCD，并在BC边上留有一扇1米宽的门．设AD边的长为x米，矩形花圃的面积为S平方米．
(1)、求S与x之间的函数关系式．(2)、若墙长a＝30米，求S的最大值．22. 如图，在正方形ABCD中，M是AB边的中点，E是AD边上的一点，且EM⊥CM，求证：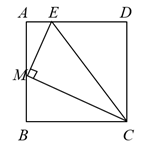
(1)、△AEM∽△BMC；(2)、；(3)、CM平分∠BCE．23. 如图1所示，已知抛物线与x轴的交点为A、B（点A在点B的左侧），与y轴的交点为C，顶点为M．
(1)、直接写出B、C、M三点的坐标，及直线BC的解析式（不写过程）；(2)、如图2，平行于x轴的直线l与直线BC相交于点D（x1 ， y1），与抛物线相交于点E（x2 ， y2）和点F（x3 ， y3），设w＝x1+x2+x3 ， 若x1＜x2＜x3 ， 求w的取值范围；(3)、在第一象限内，抛物线上是否存在一点P，连接OP交BC于点Q，使OQ：PQ的值最小？若存在，请求出点P的坐标；若不存在，请说明理由．