安徽省芜湖市市区2021-2022学年八年级上学期期中数学试题
试卷更新日期：2022-09-13 类型：期中考试
一、选择题
-
1. 手机已逐渐成为人们日常通讯的主要工具，其背后离不开通讯运营商的市场支持，下图展现的是我国四大通讯运营商的企业图标，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 下面四个图形中，线段BE能表示三角形ABC的高的是（ ）A、
B、
C、
D、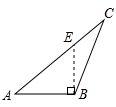
3. 如图所示，两个三角形全等，其中已知某些边的长度和某些角的度数，则x=（ ）．
A、55° B、60° C、65° D、45°4. 如图，在△ABC中，DE是AC的垂直平分线，AE=3cm，△ABD的周长为13cm，则△ABC的周长为（ ）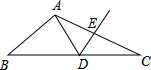
A、16cm B、13cm C、19cm D、10cm5. 如图，于点D，于点E，下列条件：①OP是的平分线；②；③；④；其中能够证明的条件的个数有（ ）
A、1个 B、2个 C、3个 D、4个6. 下图是课本中作一个角等于已知角的方法，这种作法的依据是（ ）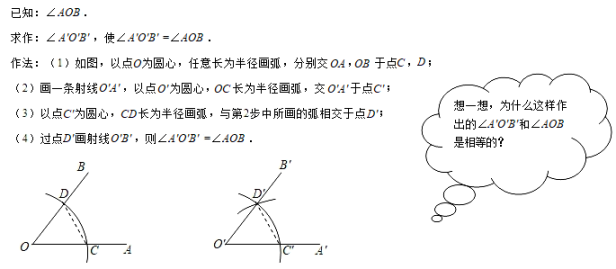
A、SSS B、SAS C、AAS D、ASA7. 如图，王师傅用六根木条钉成一个六边形木框，要使它不变形，至少还要再钉上________根木条（ ）
A、2 B、3 C、4 D、58. 一块含30°角的直角三角尺与直尺的摆放位置如图所示，若 ， 则的度数为（ ）．
A、28° B、38° C、58° D、32°9. 如图，AB，CD相交于点E，且AB=CD，试添加一个条件使得△ADE≌△CBE．现给出如下五个条件：①∠A=∠C；②∠B=∠D；③AE=CE；④BE=DE；⑤AD=CB．其中符合要求有（ ）
A、2个 B、3个 C、4个 D、5个10. 如图，∠ABC＝∠ACB，BD、CD分别平分△ABC的内角∠ABC、外角∠ACP，BE平分外角∠MBC交DC的延长线于点E．以下结论：①∠BDE＝∠BAC；②DB⊥BE；③∠BDC＋∠ABC＝90°；④∠BAC＋2∠BEC＝180°．其中正确的结论有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 一等腰三角形的底边长为 ， 一腰上的中线把三角形的周长分为两部分，其中一部分比另一部分长 ， 那么这个三角形的周长为 ．12. 如图平分 ， 平分 ， 若 ， ， ．
13. 在一个凸n边形的纸板上切下一个三角形后，剩下一个内角和为1080°的多边形，则n的值为 ．14. 如图，的度数为 ．
三、解答题
-
15. 如图，点B，C，D在同一条直线上，∠B=∠D=90°，△ABC≌△CDE，AB=6，BC=8，CE=10.
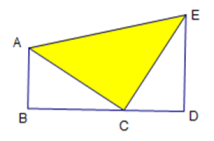(1)、求△ABC的周长；(2)、求△ACE的面积.16. 如果一个多边形的每一个外角都相等，且比内角小 ，求这个多边形的边数和内角和.17. 在如图所示的正方形网格中，每个小正方形的边长为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A，C的坐标分别为 ．
（ 1 ）请在如图所示的网格内作出x轴、y轴；
（ 2 ）请作出∆ABC关于y轴对称的∆ ， 并写出点的坐标；
（ 3 ）求出∆的面积．
18. 如图∠BAC=∠DAE，∠ABD=∠ACE，BD=CE. 求证.AB=AC．
19. 如图，已知，是的平分线，且交的延长线于点E．
求证： ．
20. 如图，四边形ABCD中，CD＝CB，AC平分∠DAB，CH⊥AB于点H.
(1)、求证：∠ADC＋∠B＝180°；(2)、若AD＝3，AB＝8，求AH的长.21. 在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°，E，F分别是BC，CD上的点，且∠EAF＝60°，探究图中线段BE，EF，FD之间的数量关系，并说明理由？
22.
(1)、阅读理解：如图1，在△ABC中，若AB＝10，BC＝8，求AC边上的中线BD的取值范围．小聪同学是这样思考的：延长BD至E，使DE＝BD，连结CE．利用全等将边AB转化到CE，在△BCE中利用三角形三边关系即可求出中线BD的取值范围．在这个过程中小聪同学证三角形全等用到的判定方法是；中线BD的取值范围是 ．(2)、问题解决：如图2，在△ABC中，点D是AC的中点，点M在AB边上，点N在BC边上，若DM⊥DN，求证：AM＋CN＞MN．(3)、问题拓展：如图3，在△ABC中，点D是AC的中点，分别以AB，BC为直角边向△ABC外作等腰直角三角形ABM和等腰直角三角形BCN，其中∠ABM＝∠NBC＝90°，连接MN，探索BD与MN的关系，并说明理由．