云南省昆明市西山区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-13 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 现实世界中，对称现象无处不在，中国的方块字中有些也只有对称性，下列汉字是轴对称图形的是（   ）
    A、 B、 C、 D、

    查看试题解析

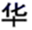  • 2. 如图，AD，BE，CF依次是△ABC的高、中线和角平分线，下列表达式中错误的是（       ）

    A、AE＝CE B、∠ADC＝90° C、∠CAD＝∠CBE D、∠ACB＝2∠ACF

    查看试题解析

  • 3. 若一个正多边形的各个内角都是140°，则这个正多边形是（   ）
    A、正七边形 B、正八边形 C、正九边形 D、正十边形

    查看试题解析

  • 4. 一天课间，顽皮的小明同学拿着老师的等腰直角三角板玩，不小心将三角板掉到两根柱子之间，如图所示，这一幕恰巧被数学老师看见了，于是有了下面这道题：如果每块砖的厚度a＝8cm，则DE的长为（       ）

    A、40cm B、48cm C、56cm D、64cm

    查看试题解析

  • 5. 已知，如图，△ABC中，AD是角平分线，DE⊥AB，DF⊥AC，垂足分别是E、F．下列说法：①DE＝DF，②AE＝AF，③AD平分∠EDF；④AD⊥BC，⑤图中共有3对全等三角形．其中正确的有（       ）

    A、2个 B、3个 C、4个 D、5个

    查看试题解析

  • 6. 在平面直角坐标系内，P（2x﹣6，5﹣x）关于x轴对称的对称点在第四象限，则x的取值范围为（  ）
    A、3＜x＜5 B、x＜3 C、5＜x D、﹣5＜x＜3

    查看试题解析

  • 7. 如图， CE 是 △ABC 的外角 ∠ACD 的平分线， CE 交 BA 的延长线于点 E ， ∠B=35° ， ∠E=25° ，则 ∠ACD 的度数为（    ）

    A、100° B、110° C、120° D、130°

    查看试题解析

  • 8. 如图所示的正方形网格中，网格的交点称为格点，已知 A ， B 是两格点，如果 C 也是图中的格点，且使得 ΔABC 为等腰三角形，则符合条件的点 C 的个数是（  ）

    A、6 B、7 C、8 D、9

    查看试题解析

二、填空题

  • 9. 图①是将木条用钉子钉成的四边形和三角形木架，拉动木架，观察图②中的变动情况，说一说，其中所蕴含的数学原理是 ．

    查看试题解析

  • 10. 如图，小林从P点向西直走8米后，向左转，转动的角度为α，再走8米，如此重复，小林共走了72米回到点P，则α为.

    查看试题解析

  • 11. 如图，点O在△ABC内且到三边的距离相等．若∠A＝58°，则∠BOC＝度．

    查看试题解析

  • 12. 如图，AB，CD相交于点E，若△ABC≌△ADE，∠BAC＝28°，则∠B的度数是 ．

    查看试题解析

  • 13. 如图，在网格图中选择一个格子涂阴影，使得整个图形是以虚线为对称轴的轴对称图形，则把阴影涂在图中标有数字的格子内．

    查看试题解析

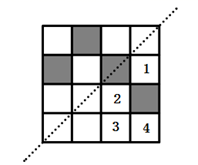  • 14. 如图，△ABC是边长6cm的等边三角形，动点P、Q同时从A、B两点出发，分别在AB、BC边上均速移动，它们的速度分别为Vp=2cm/s，VQ=1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间为ts，则当t=s时，△PBQ为直角三角形．

    查看试题解析

三、解答题

  • 15. 一个多边形的内角和比它的外角和的3倍少180°，求这个多边形的边数和内角和．

    查看试题解析

  • 16. 如图所示，

    ⑴作出△ABC关于y轴对称的图形△A1B1C1；

    ⑵在x轴上确定一点P，使得PA+PC最小．

    查看试题解析

  • 17. 已知：如图，AB＝DE，AC＝DF，BE＝CF．求证：∠A＝∠D．

    查看试题解析

  • 18. 一个等腰三角形的周长是28cm．
    (1)、已知腰长是底边长的3倍，求各边的长；
    (2)、已知其中一边长为6cm，求各边的长．

    查看试题解析

  • 19. 已知，如图，BD是∠ABC的平分线，AB＝BC，点P在BD上，PM⊥AD，PN⊥CD，垂足分别是M、N．试说明：PM＝PN．

    查看试题解析

  • 20. 如图，在△ABC中，AB＝AC ， 点D、E、F分别在AB、BC、AC边上，且BE＝CF ， BD＝CE ．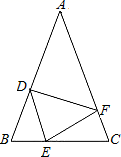

    (1)、求证：△DEF是等腰三角形；
    (2)、当∠A＝40°时，求∠DEF的度数．

    查看试题解析

  • 21. 如图，在 △ABC 中， AC<AB<BC .
    (1)、已知线段AB的垂直平分线与BC边交于点P，连结AP

    求证： ∠APC=2∠B ；

    (2)、以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连结AQ，若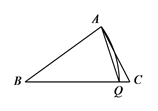 ∠AQC=3∠B ，求 ∠B 的度数.

    查看试题解析

  • 22. 如图，已知△ABC中，AB＝AC＝24厘米，∠ABC＝∠ACB，BC＝16厘米，点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动.同时，点Q在线段CA上由C点以a厘米/秒的速度向A点运动.设运动的时间为t秒.

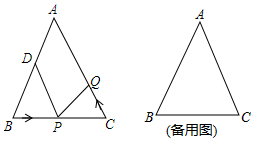    (1)、直接写出：

    ①BD＝厘米；

    ②BP＝厘米；

    ③CP＝厘米；

    ④CQ＝厘米；

    （可用含t、a的代数式表示）

    (2)、若以D，B，P为顶点的三角形和以P，C，Q为顶点的三角形全等，试求a、t的值.

    查看试题解析

  • 23. 阅读下面材料：

    【原题呈现】如图1，在△ABC中，∠A＝2∠B，CD平分∠ACB，AD＝2.2，AC＝3.6，求BC的长．

    【思考引导】因为CD平分∠ACB，所以可在BC边上取点E，使EC＝AC，连接DE．这样很容易得到△DEC≌△DAC，经过推理能使问题得到解决（如图2）．

    【问题解答】

    (1)、参考提示的方法，解答原题呈现中的问题；
    (2)、拓展提升：如图3，已知△ABC中，AB＝AC，∠A＝20°，BD平分∠ABC，BD＝2.3，BC＝2．求AD的长．

    查看试题解析