辽宁省盘锦市2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-13 类型:期中考试
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在Rt△ABC中,∠C=90°,DE是AB的垂直平分线,且∠BAD:∠BAC=1:2,则∠B的度数为( )
2. 如图,在Rt△ABC中,∠C=90°,DE是AB的垂直平分线,且∠BAD:∠BAC=1:2,则∠B的度数为( )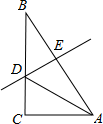 A、30° B、45° C、60° D、75°3. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若AD=3,△ACE的周长为13,则△ABC的周长为( )
A、30° B、45° C、60° D、75°3. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若AD=3,△ACE的周长为13,则△ABC的周长为( ) A、19 B、16 C、29 D、184. 下列运算正确的是( )A、(a+b)2=a2+b2 B、(-a2)a3=a6 C、(-2x2)3=-8x6 D、4a2-(2a)2=2a25. 下列分式中,属于最简分式的是( )A、 B、 C、 D、6. 等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为( )A、65° B、105° C、55°或105° D、65°或115°7. 如图,已知△ABC是等边三角形,点D是AB边中点,过D作DE⊥AC于点E,AB=10,则EC长为( )
A、19 B、16 C、29 D、184. 下列运算正确的是( )A、(a+b)2=a2+b2 B、(-a2)a3=a6 C、(-2x2)3=-8x6 D、4a2-(2a)2=2a25. 下列分式中,属于最简分式的是( )A、 B、 C、 D、6. 等腰三角形一腰上的高与另一腰的夹角为25°,则顶角的度数为( )A、65° B、105° C、55°或105° D、65°或115°7. 如图,已知△ABC是等边三角形,点D是AB边中点,过D作DE⊥AC于点E,AB=10,则EC长为( )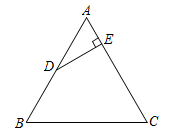 A、2.5 B、5 C、7 D、7.58. 在△ABC中,∠BAC=105°,AD⊥BC于点D,且点D在AC的垂直平分线上,DE⊥AB于点E,AE=2,则BE的长为( )
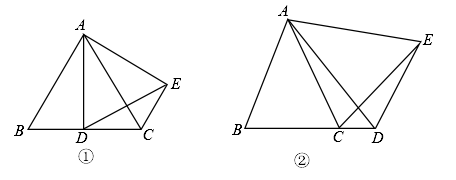
A、2.5 B、5 C、7 D、7.58. 在△ABC中,∠BAC=105°,AD⊥BC于点D,且点D在AC的垂直平分线上,DE⊥AB于点E,AE=2,则BE的长为( ) A、4 B、6 C、7 D、89. 如图,在△ABC中,AB=AC,尺规作图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D;(2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中∠BAD=∠CAD △BCD是等边三角形AD垂直平分BC ④S四边形=AD·BC错误的有( )个
A、4 B、6 C、7 D、89. 如图,在△ABC中,AB=AC,尺规作图,(1)分别以B,C为圆心,BC长为半径作弧,两弧交于点D;(2)作射线AD,连接BD,CD.根据以上作图过程及所作图形,下列结论中∠BAD=∠CAD △BCD是等边三角形AD垂直平分BC ④S四边形=AD·BC错误的有( )个 A、0 B、1 C、2 D、310. 若x-y=7,xy=2,则x2+y2值是( )A、53 B、45 C、47 D、51
A、0 B、1 C、2 D、310. 若x-y=7,xy=2,则x2+y2值是( )A、53 B、45 C、47 D、51二、填空题
-
11. 若分式的值为0,则x= .12. 若点P(a,-3)与点Q(1,b)关于x轴对称,则ab=13. 已知3m+2×92m-1×27m=98 , 则m=14. 如图,Rt△ABC中,∠ACB=90°,∠B=42°,将其折叠使点A落在BC边上的 处,折痕为CD,则=
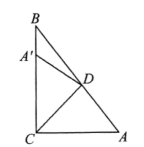 15. 如图,在△ABC中,∠BAC=110°,若MP、NQ分别垂直平分AB、AC,则∠PAQ=
15. 如图,在△ABC中,∠BAC=110°,若MP、NQ分别垂直平分AB、AC,则∠PAQ= 16. 化简=17. 如图,中,∠A=30°,AB=AC,D、E分别是AC、AB上两点,且BD=BE=BC,连接DE,则∠BDE=
16. 化简=17. 如图,中,∠A=30°,AB=AC,D、E分别是AC、AB上两点,且BD=BE=BC,连接DE,则∠BDE= 18. 已知△ABC的某两个内角的比是4:7且AB=AC,BD垂直AC于D,BE平分∠ABC交AC于点E,则∠EBD的大小是
18. 已知△ABC的某两个内角的比是4:7且AB=AC,BD垂直AC于D,BE平分∠ABC交AC于点E,则∠EBD的大小是三、解答题
-
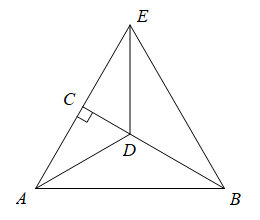
19. 已知3a=4,3b=5,3c=8(1)、填空:32a=(2)、求32a+b-c的值20. 计算下列各式(1)、2(2-1)+3(2+2)(2)、4(+1)2-(2+5)(2-5)(3)、3221. 把下列各式因式分解(1)、(2)、(3)、22. 计算下列各式(1)、(- )2·(- )3÷(-ab)4(2)、·23. 先化简,再求值(1)、已知 , 求代数式+1)--1)-7的值(2)、(+2)2+(-2)(2-)-(x+2)(-2)-42 , 其中=1,=224. 如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.求证:OE垂直平分BD.
 25. 如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
25. 如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.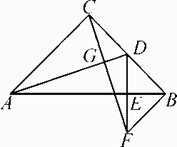 (1)、求证:AD⊥CF;(2)、连接AF,试判断△ACF的形状,并说明理由.
(1)、求证:AD⊥CF;(2)、连接AF,试判断△ACF的形状,并说明理由.