辽宁省大连市甘井子区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-13 类型:期中考试
一、单选题
-
1. 下列图形中具有稳定性的是( )A、直角三角形 B、长方形 C、正方形 D、平行四边形2. 第24届冬奥会将于2022年2月在北京和张家口举办,下列四个图分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 如图, , 和是对应角,和是对应边,其他对应边及对应角正确的是( )
3. 如图, , 和是对应角,和是对应边,其他对应边及对应角正确的是( ) A、和是对应角 B、和是对应角 C、和是对应边 D、和是对应边4. 如图, , , 是的三条中线,以下结论正确的是( )
A、和是对应角 B、和是对应角 C、和是对应边 D、和是对应边4. 如图, , , 是的三条中线,以下结论正确的是( ) A、 B、 C、 D、5. 若点与点N关于y轴对称,则点N的坐标是( )A、 B、 C、 D、6. 如图,AC⊥CB,DB⊥CB,垂足分别为C,B,AB=DC,可证得△ABC≅△DCB,则证明全等的依据是( )
A、 B、 C、 D、5. 若点与点N关于y轴对称,则点N的坐标是( )A、 B、 C、 D、6. 如图,AC⊥CB,DB⊥CB,垂足分别为C,B,AB=DC,可证得△ABC≅△DCB,则证明全等的依据是( ) A、 B、 C、 D、7. 在中, , , 则的度数是( )A、 B、 C、 D、8. 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD相交于点G,则下列关系正确的是( )
A、 B、 C、 D、7. 在中, , , 则的度数是( )A、 B、 C、 D、8. 如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD相交于点G,则下列关系正确的是( ) A、 B、且 C、 D、9. 如图所示,由三角形两边的和大于第三边,可得到的结论是( )
A、 B、且 C、 D、9. 如图所示,由三角形两边的和大于第三边,可得到的结论是( ) A、 B、 C、 D、10. 如图,在中, , , 则下列结论正确的是( )
A、 B、 C、 D、10. 如图,在中, , , 则下列结论正确的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 如图, , 若用“边边边”证明 , 则需要添加的条件是 .
 12. 如图,在中, , , 点在的延长线上,则等于 .
12. 如图,在中, , , 点在的延长线上,则等于 . 13. 如图,在中,是的垂直平分线, , , 则的周长为 .
13. 如图,在中,是的垂直平分线, , , 则的周长为 . 14. 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=5,DE=2.7,则BE= .
14. 如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为D,E,AD=5,DE=2.7,则BE= . 15. 一个多边形的内角和比四边形的内角和多 , 并且这个多边形的各内角都相等,则这个多边形的每个外角等于 .16. 如图,在等边△ABE中,AC⊥BE,CD⊥AB,垂足分别为C,D,AE=a,则AD= . (请用含的代数式表示)
15. 一个多边形的内角和比四边形的内角和多 , 并且这个多边形的各内角都相等,则这个多边形的每个外角等于 .16. 如图,在等边△ABE中,AC⊥BE,CD⊥AB,垂足分别为C,D,AE=a,则AD= . (请用含的代数式表示)
三、解答题
-
17. 如图,在△ABC中,∠B=75°,AD⊥BC,∠C=∠CAD,求∠C,∠BAC的度数.
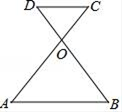
 18. 如图,已知AC和BD相交于点O,且AB∥DC,OA=OB.
18. 如图,已知AC和BD相交于点O,且AB∥DC,OA=OB.求证:OC=OD.
 19. 如图,点E , F在BC上,AB=DC , ∠A=∠D , ∠B=∠C .
19. 如图,点E , F在BC上,AB=DC , ∠A=∠D , ∠B=∠C .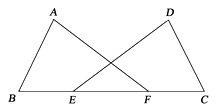
求证:BE=FC.
20. 如图,在平面直角坐标系中,的顶点坐标分别为 , , . (1)、在图中画出关于x轴对称的图形 , 并写出三个顶点的坐标: , , ;(2)、若关于轴对称的图形 , 不用画图请直接写出三个顶点的坐标: , , ;(3)、关于y轴对称的图形再关于x轴对称,得到的图形为 , 点为边上的任意一点,它在上的对应点为 , 则的坐标为 . (用含m和n的式子表示)21. 如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠BAC=50°,∠C=60°,求∠DAC和∠BOA的度数.
(1)、在图中画出关于x轴对称的图形 , 并写出三个顶点的坐标: , , ;(2)、若关于轴对称的图形 , 不用画图请直接写出三个顶点的坐标: , , ;(3)、关于y轴对称的图形再关于x轴对称,得到的图形为 , 点为边上的任意一点,它在上的对应点为 , 则的坐标为 . (用含m和n的式子表示)21. 如图,在△ABC中,AD是高,AE,BF是角平分线,它们相交于点O,∠BAC=50°,∠C=60°,求∠DAC和∠BOA的度数. 22. 如图,在△ABC和△A'B'C'中,AB=A'B',BC=B'C',AD和A'D'分别是边BC和B'C'上的中线,且AD=A'D'.求证:∠C=∠C'.
22. 如图,在△ABC和△A'B'C'中,AB=A'B',BC=B'C',AD和A'D'分别是边BC和B'C'上的中线,且AD=A'D'.求证:∠C=∠C'. 23. 如图△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.求证:DB=DE.
23. 如图△ABC是等边三角形,BD是中线,延长BC到E,使CE=CD.求证:DB=DE.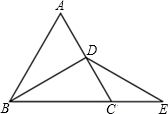 24. 如图, , 都是等边三角形, , .
24. 如图, , 都是等边三角形, , . (1)、求证:;(2)、猜想 , 的位置关系,并证明;(3)、若将“ , ”改为“ , ”,其他条件不变,请直接写出的度数(用含n的式子表示).25. 在中, , , 点 , 分别在射线和射线上,点F在线段上,与相交于点G,且 .
(1)、求证:;(2)、猜想 , 的位置关系,并证明;(3)、若将“ , ”改为“ , ”,其他条件不变,请直接写出的度数(用含n的式子表示).25. 在中, , , 点 , 分别在射线和射线上,点F在线段上,与相交于点G,且 . (1)、如图1,当点D与点B重合,点E在线段上时,求证:;(2)、如图2,当点D,E分别在 , 延长线上, , 垂足为P,请补全图形.
(1)、如图1,当点D与点B重合,点E在线段上时,求证:;(2)、如图2,当点D,E分别在 , 延长线上, , 垂足为P,请补全图形.①请问(1)中的结论是否成立?若成立,请证明;若不成立,请写出新的数量关系,并证明;
②若 , (),求的值(用含k的代数式表示).
26. 如图1,在平面直角坐标中,点 , , , 其中 , 点P为线段上任意一点,连接 , 于E,于D. (1)、求证:;(2)、当时,若点 , 请你在图1中连接 , 交于点 . 求证:;(3)、若将“点P为线段上任意一点”,改为“点P为线段延长线上任意一点”,其他条件不变,连接 , , 垂足为F,交轴于点H,交轴于点N,请在图2中补全图形,求点N的坐标(用含m的代数式表示).
(1)、求证:;(2)、当时,若点 , 请你在图1中连接 , 交于点 . 求证:;(3)、若将“点P为线段上任意一点”,改为“点P为线段延长线上任意一点”,其他条件不变,连接 , , 垂足为F,交轴于点H,交轴于点N,请在图2中补全图形,求点N的坐标(用含m的代数式表示).