辽宁省朝阳市北票市2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数中，最小的数是（）

A、－3 B、3 C、 $\frac{1}{3}$ D、- $π$

查看试题解析
2. 在下列各数0， $\frac{1}{3}$ ， 3.14， $π$ ， 0.731， $\sqrt{2}$ 中，无理数的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
3. 与数轴上的点一一对应的是

A、有理数 B、无理数 C、实数 D、正数和负数

查看试题解析
4. 在平面直角坐标系中，点（5，-7）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 点A(-3，4)关于y轴对称的点的坐标是（）

A、(3， -4) B、(-3， -4) C、(3， 4) D、(-4， -3)

查看试题解析
6. 如图：在△ABC中，∠C＝90°，AB＝13，BC＝5，则以AC为直径的半圆面积为（）

A、6π B、12π C、36π D、18π

查看试题解析
7. 已知△ABC为直角三角形，在下列四组数中，不可能是它的三边长的一组是（）

A、3，4，5 B、6，8，10 C、5，12，13 D、3，3，5

查看试题解析
8. 下列说法正确的是（）

A、－4没有立方根 B、1的立方根为±1 C、5的立方根为 $\sqrt[3]{5}$ D、 $\frac{1}{36}$ 的立方根是 $\frac{1}{6}$

查看试题解析
9. 下列函数：①y=8x；②y=- $\frac{x}{8}$ ；③y=2x²；④y=-2x+1．其中是一次函数的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
10. 已知一次函数 $y = k x + b$ 的图象如图示，则k，b的取值范围是（）

A、 $k < 0 ， b > 0$ B、 $k < 0 ， b < 0$ C、 $k > 0 ， b > 0$ D、 $k > 0 ， b < 0$

查看试题解析

二、填空题

11. 计算 $\sqrt{32}$ - $\sqrt{8}$ =.

查看试题解析
12. 比较大小（填“>、<或＝”）： $\sqrt{5}$ 2 $\frac{\sqrt{5} - 1}{2}$ $\frac{1}{2}$

查看试题解析
13. 若函数y=(a-1)x+ $a^{2}$ -1是正比例函数，则a= ．

查看试题解析
14. 在坐标系中，已知两点A（3，-2）、B（-3，-2），则直线AB与x 轴的位置关系是．

查看试题解析
15. 如图，在△ABC中，AB＝10，AC＝13，AD⊥BC，垂足为D，M为AD上任一点，则MC²﹣MB²等于．

查看试题解析
16. 如图，一个圆柱体高8 cm，底面半径2 cm，蚂蚁在圆柱表面从点A爬到点B处，要爬行的最短路程是cm

查看试题解析
17. 若实数a，b满足 $\sqrt{a + 1} + \sqrt{a + b} = 0$ ，则代数式 $a^{2021} + b^{2022}$ = ．

查看试题解析
18. 已知点A(a，0)和点B(0，4)，且直线AB与坐标轴围成的三角形的面积10，则a的值是．

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{\frac{1}{3}} + \sqrt{27} \times \sqrt{9}$ ；

(2)、 ${(2 - \sqrt{3})}^{0} - \sqrt[3]{- 64} - {(\frac{1}{4})}^{- 1} + | \sqrt{3} - 2 |$ ；

(3)、( $\sqrt{5} - \sqrt{7}) (\sqrt{5} + \sqrt{7}) + 2$ ；

(4)、 $\frac{2}{3} \sqrt{20} \times (- \frac{1}{3} \sqrt{48}) \div \sqrt{2 \frac{2}{3}}$

查看试题解析
20. 已知函数y＝ $\frac{1}{2}$ x－2，画图像回答：

(1)、当x的值增加时，y的值如何变化？

(2)、图象与x轴，y轴的交点坐标分别是多少？

(3)、求出该图象与x轴，y轴所围成的三角形的面积．

查看试题解析
21. 如图，方格纸中每个小正方形的边长都是1，△ABC的三个顶点都在格点上，如果用（0，0）表示A点的位置，用（4，-1）表示B点的位置．
（ 1 ）画出直角坐标系；
（ 2 ）画出与△ABC关于x轴对称的图形△DEF；
（ 3 ）分别写出点D、E、F的坐标．

查看试题解析
22. 小明想知道学校旗杆的高，他发现旗杆顶端的绳子垂到地面还多1米，当他把绳子的下端拉开5米后，发现下端刚好接触地面.求旗杆的高度.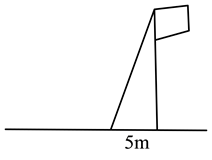

查看试题解析
23. 如图，等腰直角三角板如图放置．直角顶点C在直线m上，分别过点A、B作AE⊥直线m于点E，BD⊥直线m于点D．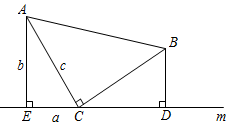
①求证： $EC = BD$ ；
②若设△AEC三边分别为a、b、c，利用此图证明勾股定理．

查看试题解析
24. 如图，折叠长方形的一边AD，使点D落在BC边上的点F处，BC=10cm，AB=8cm，求EF的长

查看试题解析
25. 某电信公司手机有两类收费标准，A类收费标准如下：不管通话时间多长，每部手机每月必须缴月租费12元，另外，通话费按0.2元/min计．B类收费标准如下：没有月租费，但通话费按0.25元/min计．

(1)、分别写出A、B两类每月应缴费用y（元）与通话时间x（min）之间的关系式；

(2)、如果手机用户预算每月交55元的话费，那么该用户选择哪类收费方式合算？

(3)、每月通话多长时间，按A、B两类收费标准缴费，所缴话费相等？

查看试题解析
26. 如图，直线y= $\frac{1}{2}$ x+3与x轴相交于点A，与y轴相交于点B

(1)、直接写出△AOB的面积；

(2)、若C为y轴上一点，且△ABC的面积是12，求点C的坐标；

(3)、若P是x轴上一点，且AB=AP，求P的坐标．

查看试题解析