吉林省吉林市永吉县2021-2022学年八年级上学期期中考试数学试题
试卷更新日期:2022-09-13 类型:期中考试
一、单选题
-
1. 下列轴对称图形中,对称轴条数最多的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在建筑工地我们常可看见如图所示,用木条EF固定矩形门框ABCD的情形.这种做法根据( )
2. 在建筑工地我们常可看见如图所示,用木条EF固定矩形门框ABCD的情形.这种做法根据( )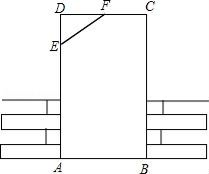 A、两点之间线段最短 B、两点确定一条直线 C、三角形的稳定性 D、矩形的四个角都是直角3. 四边形中,如果 , 则的度数是( )A、110° B、100° C、90° D、30°4. 等腰三角形ABC的周长为8cm,AB=2cm,则BC长为( )A、2cm B、3cm C、2或3cm D、4cm5. 如图,点 、 在线段 的同侧,连接 、 、 、 ,已知 ,老师要求同学们补充一个条件使 .以下是四个同学补充的条件,其中错误的是
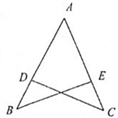
A、两点之间线段最短 B、两点确定一条直线 C、三角形的稳定性 D、矩形的四个角都是直角3. 四边形中,如果 , 则的度数是( )A、110° B、100° C、90° D、30°4. 等腰三角形ABC的周长为8cm,AB=2cm,则BC长为( )A、2cm B、3cm C、2或3cm D、4cm5. 如图,点 、 在线段 的同侧,连接 、 、 、 ,已知 ,老师要求同学们补充一个条件使 .以下是四个同学补充的条件,其中错误的是 A、 B、 C、 D、6. 如图,在中,按以下步骤作图:①分别以点B和C为圆心,适当长度(大于长的一半)为半径作圆弧,两弧相交于点M和N;②作直线交于点D,连接 . 若 , , 则的周长是( )
A、 B、 C、 D、6. 如图,在中,按以下步骤作图:①分别以点B和C为圆心,适当长度(大于长的一半)为半径作圆弧,两弧相交于点M和N;②作直线交于点D,连接 . 若 , , 则的周长是( )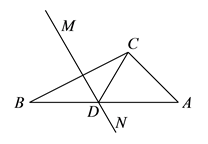 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
7. 一副三角板如图所示叠放在一起,则图中的度数为 .
 8. 点P(-2,3)关于y轴的对称点P′的坐标为 .9. 若正多边形的一个外角是45°,则该正多边形的边数是 .10. 如图,点A,F,C,D在同一条直线上, , , 请你再添加一个条件使 . 你添加的条件是 .
8. 点P(-2,3)关于y轴的对称点P′的坐标为 .9. 若正多边形的一个外角是45°,则该正多边形的边数是 .10. 如图,点A,F,C,D在同一条直线上, , , 请你再添加一个条件使 . 你添加的条件是 . 11. 如图,中,点D在BC上, , , 则的度数为 .
11. 如图,中,点D在BC上, , , 则的度数为 . 12. 在Rt△ABC中∠C=90°,∠A=30°,BC+AB=12cm , 则AB= cm .13. 如图,在Rt△ABC中,∠ACB=90°,∠B=15°,AB的垂直平分线与BC交于点D,交AB于点E,连接AD.则∠CAD的度数为 .
12. 在Rt△ABC中∠C=90°,∠A=30°,BC+AB=12cm , 则AB= cm .13. 如图,在Rt△ABC中,∠ACB=90°,∠B=15°,AB的垂直平分线与BC交于点D,交AB于点E,连接AD.则∠CAD的度数为 . 14. 如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为.
14. 如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为.
三、解答题
-
15. 如图,点D在AB上,点E在AC上,AB=AC,∠B=∠C.求证:BD=CE.
 16. 如图,点A和点C分别在的边BD,BE上,并且 , .
16. 如图,点A和点C分别在的边BD,BE上,并且 , . (1)、直接写出BC的取值范围;(2)、若 , , , 求的度数.17. 如图,在 中, ,点D在边 上,且 ,过点D作 并截取 ,且点C,E在 同侧,连接 .
(1)、直接写出BC的取值范围;(2)、若 , , , 求的度数.17. 如图,在 中, ,点D在边 上,且 ,过点D作 并截取 ,且点C,E在 同侧,连接 .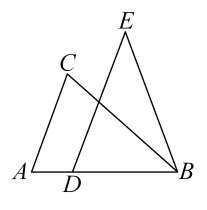
求证: .
18. 如图,在△ABC中,AB=AC,AD平分∠BAC.求证:∠DBC=∠DCB. 19. 如图①、图②、图③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B两点均为格点,按下列要求画图:
19. 如图①、图②、图③都是3×3的正方形网格,每个小正方形的顶点称为格点.A,B两点均为格点,按下列要求画图:

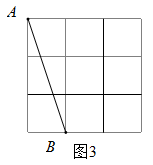 (1)、在图①中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N均为格点;(2)、在图②中,画以AB为底边的等腰 , 且C为格点;(3)、在图③中,画一个四边形ABDE,使其为轴对称图形,且D,E均为格点.20. 如图,在中, , D,E两点都在BC上,且 .
(1)、在图①中,画一条不与AB重合的线段MN,使MN与AB关于某条直线对称,且M,N均为格点;(2)、在图②中,画以AB为底边的等腰 , 且C为格点;(3)、在图③中,画一个四边形ABDE,使其为轴对称图形,且D,E均为格点.20. 如图,在中, , D,E两点都在BC上,且 . (1)、求证:;(2)、若 , , 求的度数.21. 如图,中,EF垂直平分AC,交AC于点F,交BC于点E, , 垂足为D,且 , 连接AE.
(1)、求证:;(2)、若 , , 求的度数.21. 如图,中,EF垂直平分AC,交AC于点F,交BC于点E, , 垂足为D,且 , 连接AE. (1)、求证:;(2)、若的周长为14cm, , 则DC的长为cm.22. 如图, , 于E, 交AD的延长线于F,且 .
(1)、求证:;(2)、若的周长为14cm, , 则DC的长为cm.22. 如图, , 于E, 交AD的延长线于F,且 .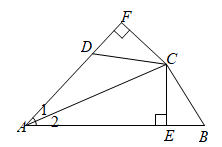 (1)、BE与DF是否相等?请说明理由;(2)、若 , ,则AB的长为cm.23. 课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示:
(1)、BE与DF是否相等?请说明理由;(2)、若 , ,则AB的长为cm.23. 课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示: (1)、求证:△ADC≌△CEB;(2)、已知DE=35cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相同)24. 如图,△ABC是等边三角形,D为AB边上任意一点,连接CD.
(1)、求证:△ADC≌△CEB;(2)、已知DE=35cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相同)24. 如图,△ABC是等边三角形,D为AB边上任意一点,连接CD. (1)、°;(2)、以BD为边作等边 , 点E在的外部(尺规作图,保留作图痕迹,不写作法);(3)、连接AE,求证: .25.
(1)、°;(2)、以BD为边作等边 , 点E在的外部(尺规作图,保留作图痕迹,不写作法);(3)、连接AE,求证: .25. (1)、四边形ABCD中,∠A=140°,∠D=80°.
(1)、四边形ABCD中,∠A=140°,∠D=80°.①如图1,若∠B=∠C,则∠C=°;
②如图2,若∠ABC的平分线BE交DC于点E,且 , 则°;
③如图3,若∠ABC和∠BCD的平分线相交于点E,则∠BEC=°;
(2)、如图3,当 , 时,若∠ABC和∠BCD的平分线交于点E,∠BEC与α,β之间的数量关系为;(3)、如图4,在五边形ABCDE中,∠A+∠B+∠E=300°,CP,DP分别平分∠BCD和∠EDC,求∠P的度数.26. 在中,∠BAC=90°, , 点D为直线BC上一动点(点D不与B,C重合),以AD为直角边在AD右侧作等腰直角三角形ADE( , ),连接CE. (1)如图1,当点D在线段BC上时,猜想:BC与CE的位置关系,并说明理由;(1)、如图2,当点D在线段CB的延长线上时,(1)题的结论是否仍然成立?说明理由;(2)、如图3,当点D在线段BC的延长线上时,结论(1)题的结论是否仍然成立?不需要说明理由.
(1)如图1,当点D在线段BC上时,猜想:BC与CE的位置关系,并说明理由;(1)、如图2,当点D在线段CB的延长线上时,(1)题的结论是否仍然成立?说明理由;(2)、如图3,当点D在线段BC的延长线上时,结论(1)题的结论是否仍然成立?不需要说明理由.