广东省清远市清新区三校2021-2022学年八年级上学期期中联合知识演练数学试题

试卷更新日期：2022-09-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下列实数中的无理数是（）

A、0.7 B、 C、π D、－8

查看试题解析
2. 点A (2，-1)关于x轴对称的点B的坐标为（）

A、(2, 1) B、(-2，1) C、(2，-1) D、(-2，- 1)

查看试题解析
3. $\sqrt{9}$ 的值是（　　）

A、﹣3 B、3或﹣3 C、3 D、9

查看试题解析
4. 下列运算正确的是（）

A、 $\sqrt{16} = 8$ B、 $\sqrt[3]{- 8} = - 2$ C、 $\sqrt{{(- 2)}^{2}} = - 2$ D、 $\sqrt{9 + \frac{1}{4}} = 3 + \frac{1}{2}$

查看试题解析
5. 下列各点位于平面直角坐标系内第二象限的是（）

A、 $(1 ， 2)$ B、 $(- 1 ， 2)$ C、 $(1 ， - 2)$ D、 $(- 1 ， - 2)$

查看试题解析
6. 如图，分别以 $R t △ A B C$ 三边向外作三个正方形，其面积分别用 $S_{1}$ 、 $S_{2}$ 、 $S_{3}$ 表示，若 $S_{3} = 2$ ， $S_{2} = 7$ ，那么 $S_{1} =$ （）

A、9 B、5 C、14 D、3.5

查看试题解析
7. 下列各组中的三个数值，能够构成直角三角形的是（　　）

A、2，3，4 B、60，61，10 C、 $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{5}$ D、3，4，5

查看试题解析
8. 如下图，数轴上点A所表示的数是（）

A、 $\sqrt{3}$ B、 $\sqrt{3} - 1$ C、 $\sqrt{5}$ D、 $\sqrt{5} - 1$

查看试题解析
9. 如图，大正方形是由4个小正方形组成，小正方形的边长为2，连接小正方形的三个顶点，得到△ABC，则△ABC的面积为（　　）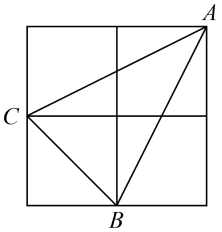

A、4 B、6 C、8 D、10

查看试题解析
10. 如图，等腰直角三角形纸片ABC中，∠C=90°，把纸片沿EF对折后，点A恰好落在BC上的点D处，点CE=1，AC=4，则下列结论一定正确的个数是（）
①∠CDE=∠DFB；②BD＞CE；③BC= $\sqrt{2}$ CD；④△DCE与△BDF的周长相等．

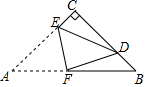A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 比较大小： $\sqrt{17}$ 5．（填“>”或“<”或“=”）

查看试题解析
12. 计算： $\sqrt{4} - \sqrt{1} =$ ．

查看试题解析
13. 点 $P (m + 3 ， m + 1)$ 在直角坐标系的x轴上，则点P坐标为．

查看试题解析
14. 点A（3，﹣4）到x轴的距离是

查看试题解析
15. 已知 $\sqrt{x + 2} + {(x + y - 4)}^{2} = 0$ ，则 $x + y =$ ．

查看试题解析
16. 小明家离学校距离3千米，上学时小明骑自行车以10千米/小时速度走了x 小时，这时离学校还有y千米．写出y与x的函数表达式．

查看试题解析
17. 如图，一个圆柱形工艺品高为16厘米，底面周长12厘米，现在需要从下底的A处绕侧面一周，到上底B（A的正上方）处镶嵌一条金丝，则金丝至少厘米．

查看试题解析

三、解答题

18. 计算： $(\sqrt{5} - \sqrt{2}) (\sqrt{5} + \sqrt{2}) - {(\sqrt{3} - 1)}^{2}$

查看试题解析
19. 已知△ABC在平面直角坐标系中的位置如图所示．（图中每个小方格边长均为1个单位长度）．

(1)、直接写出A、B、C三点坐标．A点， B点， C点；

(2)、作出△ABC关于y轴对称的△A₁B₁C₁ ．

查看试题解析
20. 如图，在 $△ A B C$ 中，D是 $B C$ 上的一点，若 $A B = 10$ ， $B D = 6$ ， $A D = 8$ ， $A C = 17$ ，求线段CD的长．

查看试题解析
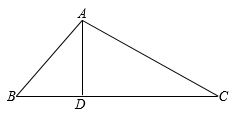21. 生活经验表明，靠墙摆放梯子时，若梯子底端离墙的距离约为梯子长度的 $\frac{1}{3}$ ，则梯子比较稳定，如图，AB为一长度为6米的梯子．

(1)、当梯子稳定摆放时，它的顶端能达到5.7米高的墙头吗？（温馨提示： $\sqrt{2}$ ≈1.414）

(2)、如图2，若梯子底端向左滑动使OD=3 $\sqrt{2}$ 米，那么梯子顶端将下滑多少米？（结果保留1位小数）

查看试题解析
22. 如图所示，在平面直角坐标系中，A（0，4），B（－2，2），C（3，0）．

(1)、在平面直角坐标系中画出△ABC；

(2)、求△ABC的面积．

查看试题解析
23. 两家商店出售同样的茶壶和茶杯，茶壶每只定价20元，茶杯每只定价5元，两家商店的优惠办法不同：甲店：买一只茶壶赠送一只茶杯；乙店：按定价的9折优惠，某顾客需购买茶壶4只，茶杯若干只（不少于4只）．

(1)、设购买茶杯数为x（只），在甲店购买的付款为y_甲（元），在乙店购买的付款数为y_乙（元），分别写出在两家商店购物的付款数与茶杯数x之间的关系式；

(2)、当购买20只茶杯时，去哪家商店购物比较合算？

查看试题解析
24. 如图，在长方形ABCD中，AB＝3，BC＝4，点E是BC边上一点，连接AE，将∠B沿直线AE折叠，使点B落在点 $B^{'}$ 处．

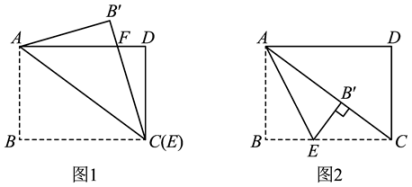(1)、如图1，当点E与点C重合时， $C B^{'}$ 与AD交于点F，求证：FA＝FC；

(2)、如图2，当点E不与点C重合，且点 $B^{'}$ 在对角线AC上时，求CE的长．

查看试题解析
25. 阅读理解，在平面直角坐标系中，P₁(x₁ ， y₁)，P₂(x₂ ， y₂)，如何求P₁P₂的距离．
如图1，作Rt△P₁P₂Q，在Rt△P₁P₂Q中， ${| P_{1} P_{2} |}^{2}$ ＝ ${| P_{1} Q |}^{2}$ ＋ ${| P_{2} Q |}^{2}$ ＝ ${(x_{2} － x_{1})}^{2} + {(y_{2} － y_{1})}^{2}$ ，所以 $| P_{1} P_{2} |$ ＝ $\sqrt{{(x_{2} － x_{1})}^{2} + {(y_{2} － y_{1})}^{2}}$ ．因此，我们得到平面上两点P₁(x₁ ， y₁)，P₂(x₂ ， y₂)之间的距离公式为 $| P_{1} P_{2} |$ ＝ $\sqrt{{(x_{2} － x_{1})}^{2} + {(y_{2} － y_{1})}^{2}}$ ．
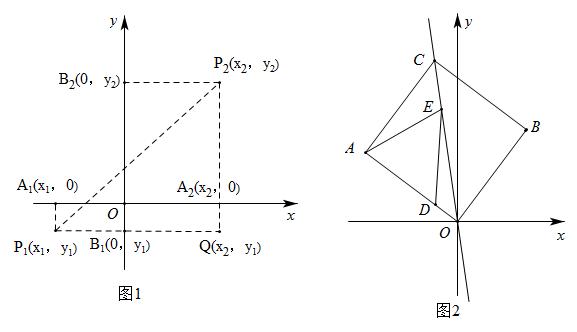
根据上面得到的公式，解决下列问题：

(1)、已知平面两点A(－3，4)，B(5，10)，求AB的距离；

(2)、若平面内三点A(－2，2)，B(5，－2)，C(1，4)，试判断△ABC的形状，说明理由；

(3)、如图2，在有对称美的正方形AOBC中，A(－4，3)，点D在OA边上，且D(－1， $\frac{3}{4}$ )，直线l经过O，C两点，点E是直线l上的一个动点，求DE＋EA的最小值．

查看试题解析