广东省揭阳市揭东区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-13 类型:期中考试
一、单选题
-
1. 在实数 , , 0.1010010001…, , 中无理数有( )A、4个 B、3个 C、2个 D、1个2. 16的平方根是( )A、±8 B、8 C、4 D、±43. 下列数据中不能确定物体的位置的是( )A、南偏西40° B、红旗小区3号楼701号 C、龙山路461号 D、东经130°,北纬54°4. 下列计算结果正确的是( )A、 B、 C、 D、5. 已知点 和 关于x轴对称,则a+b的值为( )A、 B、0 C、1 D、56. 若y=(k﹣2)x|k﹣1|+1表示一次函数,则k等于( )A、0 B、2 C、0或2 D、﹣2或07. 若点P位于平面直角坐标系第四象限,且点P到x轴的距离是1,到y轴的距离是2,则点P的坐标为( )A、 B、 C、 D、8. 满足下列条件时, 不是直角三角形的是( )A、 , , B、 C、 D、 ,9. 实数a,b在数轴上的位置如图所示,化简( )
 A、﹣b B、b C、﹣2a﹣b D、﹣2a+b10. 下列图形中,表示一次函数切与正比例函数(m,n为常数,且)的图象的是( )A、
A、﹣b B、b C、﹣2a﹣b D、﹣2a+b10. 下列图形中,表示一次函数切与正比例函数(m,n为常数,且)的图象的是( )A、 B、
B、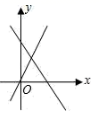 C、
C、 D、
D、
二、填空题
-
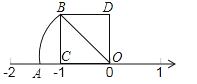
11. 的算术平方根是12. 一个实数的平方根为与 , 则这个实数是 .13. 若二次根式 在实数范围内有意义,则 的取值范围是.14. 如图,正方形ODBC中,OB= , OA=OB,则数轴上点A表示的数是
 15. a是 的整数部分,b是 的小数部分,则 ;16. 如图,有一圆柱,其高为14cm,它的底面周长为10cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,其中B离上沿2cm,则蚂蚁经过的最短路程为 .
15. a是 的整数部分,b是 的小数部分,则 ;16. 如图,有一圆柱,其高为14cm,它的底面周长为10cm,在圆柱下底面A处有一只蚂蚁,它想得到上面B处的食物,其中B离上沿2cm,则蚂蚁经过的最短路程为 .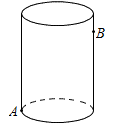 17. 在平面直角坐标系中,直线l:与x轴交于点 , 如图所示依次作正方形、正方形、…、正方形 , 使得点、、、…在直线1上,点、、、…在y轴正半轴上,则点的坐标是 .
17. 在平面直角坐标系中,直线l:与x轴交于点 , 如图所示依次作正方形、正方形、…、正方形 , 使得点、、、…在直线1上,点、、、…在y轴正半轴上,则点的坐标是 .
三、解答题
-
18. 计算:19.
△ABC在直角坐标系内的位置如图.
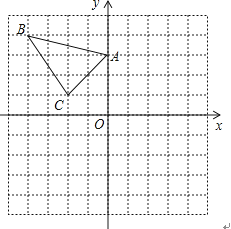 (1)、分别写出A、B、C的坐标(2)、请在这个坐标系内画出△A1B1C1 , 使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标20. 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,求CD的长.
(1)、分别写出A、B、C的坐标(2)、请在这个坐标系内画出△A1B1C1 , 使△A1B1C1与△ABC关于y轴对称,并写出B1的坐标20. 如图,有一块直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD对折,使它落在斜边AB上,且与AE重合,求CD的长. 21. 已知3a+b-1的平方根为±4,5a+2的立方根为3.(1)、求a,b的值;(2)、求2a-b+1的算术平方根.22. 如图,在四边形 中,已知 , .
21. 已知3a+b-1的平方根为±4,5a+2的立方根为3.(1)、求a,b的值;(2)、求2a-b+1的算术平方根.22. 如图,在四边形 中,已知 , .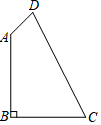 (1)、求 的度数;(2)、求四边形 的面积.23. 已知函数y=(m+1)x2-|m|+n+4.(1)、当m,n为何值时,此函数是一次函数?(2)、当m,n为何值时,此函数是正比例函数?24. 小明在解决问题:已知a= , 求2a2﹣8a+1的值,他是这样分析与解答的:
(1)、求 的度数;(2)、求四边形 的面积.23. 已知函数y=(m+1)x2-|m|+n+4.(1)、当m,n为何值时,此函数是一次函数?(2)、当m,n为何值时,此函数是正比例函数?24. 小明在解决问题:已知a= , 求2a2﹣8a+1的值,他是这样分析与解答的:∵a= .
∴a﹣2=﹣ .
∴(a﹣2)2=3,即a2﹣4a+4=3.
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据小明的分析过程,解决如下问题:
(1)、计算:= ;(2)、计算:+…+;(3)、若a= , 求2a2﹣8a+1的值.25. 在平面直角坐标系中,O为坐标原点,过点A(8,6)分别做x轴、y轴的平行线,交y轴于点B,交x轴于点C,点P是从点B出发,沿B→A→C以2个单位长度/秒的速度向终点C运动的一个动点,运动时间为t(秒).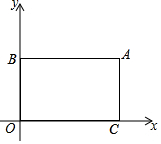 (1)、直接写出点B和点C的坐标:B( , )C( , ).(2)、当点P运动时,用含t的代数式表示线段AP的长,并写出t的取范围;(3)、点D(2,0),连结PD、AD,在(2)的条件下是否存在这样的t值,使S△APD=S四边形ABOC , 若存在,请求t值,若不存在,请说明理由.
(1)、直接写出点B和点C的坐标:B( , )C( , ).(2)、当点P运动时,用含t的代数式表示线段AP的长,并写出t的取范围;(3)、点D(2,0),连结PD、AD,在(2)的条件下是否存在这样的t值,使S△APD=S四边形ABOC , 若存在,请求t值,若不存在,请说明理由.