广东省河源市江东新区2021-2022学年八年级上学期期中数学试题

试卷更新日期：2022-09-13 类型：期中考试

进入出卷网下载

一、单选题

1. 在实数0.3，0， $\sqrt{7}$ ， $\frac{π}{2}$ ， $\frac{\sqrt{10}}{2}$ ， 123454545…中，无理数有（　　）

A、2个 B、3个 C、4个 D、5个

查看试题解析
2. 平面直角坐标系中，点P(3，-4)位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列二次根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{1}{3}}$ B、 $\sqrt{20}$ C、 $2 \sqrt{2}$ D、 $\sqrt{121}$

查看试题解析
4. 下列说法正确的是（　　）

A、－81的平方根是±9 B、任何数的平方是非负数，因而任何数的平方根也是非负数 C、任何一个非负数的平方根都不大于这个数 D、3是9的平方根

查看试题解析
5. 如图，一场大风后，一棵大树在高于地面 1 米处折断，大树顶部落在距离大树底部 3 米处的地面上，那么树高是（）

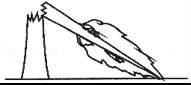A、4m B、 $\sqrt{10}$ m C、（ $\sqrt{10}$ +1）m D、（ $\sqrt{10}$ +3）m

查看试题解析
6. 如图，在平面直角坐标系中，点P的坐标为 $(- 3 ， 4)$ ，以点O为圆心，以OP长为半径画弧，交x轴的负半轴于点A，则点A的横坐标为（　　）

A、5 B、－3 C、－4 D、－5

查看试题解析
7. 如图，学校（记作A）在蕾蕾家（记作B）南偏西25°的方向上，且与蕾蕾家的距离是4km，若∠ABC＝90°，且AB＝BC，则超市（记作C）在蕾蕾家的（　　）

A、南偏东65°的方向上，相距4km B、南偏东55°的方向上，相距4km C、北偏东55°的方向上，相距4km D、北偏东65°的方向上，相距4km

查看试题解析
8. 无理数 $\sqrt{12} - \sqrt{3}$ 的大小在以下两个整数之间（）

A、1与2 B、2与3 C、3与4 D、4与5

查看试题解析
9. 在如图所示的数轴上，点B与点C关于点A对称，A，B两点对应的实数分别是 $\sqrt{2}$ 和﹣1，则点C所对应的实数是（）

A、 $1 + \sqrt{2}$ B、 $2 + \sqrt{2}$ C、 $2 \sqrt{2} - 1$ D、 $2 \sqrt{2} + 1$

查看试题解析
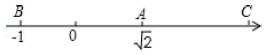10. 如图，在Rt $△$ ABC中，CA＝CB＝2，M为CA的中点，在AB上存在一点P，连接PC、PM，则 $△$ PMC周长的最小值是（　　）

A、 $\sqrt{5}$ B、 $\sqrt{3}$ C、 $\sqrt{5}$ +1 D、 $\sqrt{3}$ +1

查看试题解析

二、填空题

11. $\frac{\sqrt{3}}{3}$ 的倒数为．

查看试题解析
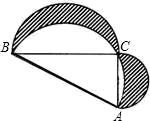
12. 函数y=kx的图象经过点P(3，－1)，则k的值为.

查看试题解析
13. 如果 $\sqrt{x - 1} + \sqrt{9 - x}$ 有意义，那么代数式 $x - 1 + \sqrt{{(9 - x)}^{2}}$ 的值为．

查看试题解析
14. 一艘轮船以16 $k m / h$ 的速度离开港口向东北方向航行，另一艘轮船同时离开港口以12 $k m / h$ 的速度向东南方向航行，它们离开港口1 小时后相距．

查看试题解析
15. 已知点 $M (3 ， a)$ 和 $N (b ， 4)$ 关于x轴对称，则 ${(a + b)}^{2021}$ 的值为．

查看试题解析
16. 如图，Rt△ABC中，AC＝5，BC＝12，分别以它的三边为直径向上作三个半圆，则阴影部分面积为．

查看试题解析
17. 如图，直线 $y = \sqrt{3} x$ ，点 $A_{1}$ 坐标为 $(1 ， 0)$ ，过点 $A_{1}$ 作x轴的垂线交直线于点 $B_{1}$ ，以原点O为圆心， $O B_{1}$ 长为半径画弧交x轴于点 $A_{2}$ ；再过点 $A_{2}$ 作x轴的垂线交直线于点 $B_{2}$ ，以原点O为圆心， $O B_{2}$ 长为半径画弧交x轴于点 $A_{3}$ ， …，按照此做法进行下去，点 $A_{n}$ 的坐标为．

查看试题解析

三、解答题

18. 计算：

(1)、 $\sqrt{8} + \sqrt{32} - \sqrt{2}$

(2)、 $(\sqrt{8} + \sqrt{3}) \times \sqrt{6}$

查看试题解析
19. 计算： $\sqrt{24} - \sqrt{18} \times \sqrt{\frac{1}{3}} + (2 - \sqrt{3})^{0}$

查看试题解析
20. 若y－1与x＋2成正比例，且当x＝2时，y＝5．

(1)、求y与x的函数关系式；

(2)、如果点 $(m ， 5)$ 在该函数图象上，求m的值．

查看试题解析
21. 在正方形网格中建立如图的平面直角坐标系 xOy，△ABC 的三个顶点都在格点上，点 A的坐标是（4，4），请解答下列问题：

（ 1 ）将△ABC 向下平移 5 单位长度，画出平移后的△A₁B₁C₁并写出点 A对应点A₁的坐标；

（ 2 ）画出△A₁B₁C₁ 关于 y 轴对称的△A₂B₂C₂并写出 A₂ 的坐标；

（ 3 ）求S△ABC．

查看试题解析
22. 已知 $6 - \sqrt{10}$ 的整数部分为a，小数部分为b，试求 $\frac{1}{6} (b - 2) (\sqrt{10} + a)$ 的值．

查看试题解析
23. 如图所示，一辆装满货物的卡车，其外形高2.5米，宽1.6米，要开进厂门形状如图的某工厂，问这辆卡车能否通过该工厂的厂门？

查看试题解析
24. 如图，在直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式 $| a - 2 | + {(b - 3)}^{2} + \sqrt{c - 4} = 0$

(1)、求a、b、c的值；

(2)、如果在第二象限内有一点P（m， $\frac{1}{2}$ ），请用含m的式子表示四边形ABOP的面积；

(3)、在（2）的条件下，是否存在点P，使四边形ABOP的面积为△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．

查看试题解析
25. 先阅读一段文字，再回答下列问题：
已知在平面内两点坐标 $P_{1} (x_{1} ， y_{1})$ ， $P_{2} (x_{2} ， y_{2})$ ，其两点间距离公式为 $P_{1} P_{2} = \sqrt{{(x_{2} - x_{1})}^{2} + {(y_{2} - y_{1})}^{2}}$ ，例如：点 $(3 ， 2)$ 和 $(4 ， 0)$ 的距离为 $\sqrt{{(3 - 4)}^{2} + {(2 - 0)}^{2}} = \sqrt{5}$ ．同时，当两点所在的直线在坐标轴上或平行于x轴或垂直于x轴距离公式可简化成 $P_{1} P_{2} = | x_{2} - x_{1} |$ 或 $P_{1} P_{2} = | y_{2} - y_{1} |$ ．

(1)、已知A、B在平行于y轴的直线上，点A的纵坐标为5，点B的纵坐标为－1，则A，B两点的距离为．

(2)、已知 $A (3 ， 5)$ ， $B (- 2 ， - 1)$ ，试求A，B两点的距离；

(3)、已知一个三角形各顶点坐标为 $A (0 ， 6)$ ， $B (- 3 ， 2)$ ， $C (3 ， 2)$ ，你能断定此三角形的形状吗？

查看试题解析