广东省佛山市南海区大沥镇2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-13 类型:期中考试
一、单选题
-
1. 在﹣ , , 0.010010001……(相邻两个1之间0的个数依次多一个),﹣0.33333……, , 2π中,无理数有( )A、1个 B、2个 C、3个 D、4个2. 各组数中,是勾股数的是( )A、9,16,25 B、0.3,0.4,0.5 C、1, , 2 D、8,15,173. 点A(﹣3,2)关于y轴的对称点的坐标为( )A、(3,2) B、(﹣3,2) C、(﹣3,﹣2) D、(﹣2,3)4. 下列运算正确的是( )A、 B、﹣=﹣ C、±=3 D、5. 已知 是方程kx+2y=-5的解,则k的值为( )A、﹣1 B、3 C、4 D、56. 如图,一次函数y=kx+b的图象经过点(2,0)、(0,1),则下列结论正确的是( )
 A、k=1 B、关于x的方程kx+b=0的解是x=2 C、b=2 D、关于x的方程kx+b=0的解是x=17. 以方程组 的解为坐标的点 在平面直角坐标系中的位置是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图是我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积41,小正方形的面积是1,直角三角形的短直角边为a,较长的直角边为b,那么(a+b)2的值为( )
A、k=1 B、关于x的方程kx+b=0的解是x=2 C、b=2 D、关于x的方程kx+b=0的解是x=17. 以方程组 的解为坐标的点 在平面直角坐标系中的位置是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 如图是我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积41,小正方形的面积是1,直角三角形的短直角边为a,较长的直角边为b,那么(a+b)2的值为( ) A、25 B、41 C、62 D、819. 下列说法中:
A、25 B、41 C、62 D、819. 下列说法中:①一次函数y=kx+b,若k>0,b<0,那么它的图象过第一、二、三象限;
②函数y=﹣6x是一次函数,且y随着x的增大而减小;
③已知一次函数的图象与直线y=﹣x+1平行,且过点(8,﹣2),那么此一次函数的解析式为y=﹣x+6;
④若一次函数y=(m﹣6)x+5中,y随x增大而减小,则m的取值范围是m>6.
正确的有( )个
A、1 B、2 C、3 D、410. 如图,在平面直角坐标系中,点A1 , A2 , A3在直线y= x+b上,点B1 , B2 , B3在x轴上,△OA1B1 , △B1A2B2 , △B2A3B3都是等腰直角三角形,若已知点A1(1,1),则点A3的纵坐标是( )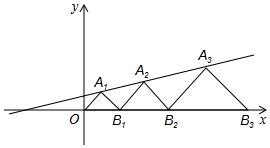 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 25的平方根是 .12. 比较实数的大小:2(填“>”、“<”或“=”).13. 已知点P(m+2,2m﹣4)在y轴上,则点P的坐标是 .14. 若 是方程2x+y=10的解,求6a+3b﹣4的值是 .15. 当k=时,函数y=(k﹣1)x+k2﹣1是一个正比例函数.16. 若关于x,y的方程组与的解相同,则的值为 .17. 如图,直线 交x轴于点A,交y轴于点B,点C为线段OB上一点,将 沿着直线AC翻折,点B恰好落在x轴上的D处,则 的面积为 .

三、解答题
-
18. 计算:﹣(2+1)2 .19. 解方程组: .20. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点A的坐标为(1,4),点B的坐标为(2,0),点C的坐标为(4,0).
 (1)、在如图的直角坐标系中画出A,B,C三点,并作出△ABC关于x轴对称的△A1B1C1 , 写出点A1坐标;(2)、线段APx轴且AP=4,请直接写出点P的坐标.21. 已知一次函数y=﹣x+2.
(1)、在如图的直角坐标系中画出A,B,C三点,并作出△ABC关于x轴对称的△A1B1C1 , 写出点A1坐标;(2)、线段APx轴且AP=4,请直接写出点P的坐标.21. 已知一次函数y=﹣x+2. (1)、在给定的直角坐标系中画出一次函数y=﹣x+2的图象;(2)、根据图象回答,当x时,y>0;
(1)、在给定的直角坐标系中画出一次函数y=﹣x+2的图象;(2)、根据图象回答,当x时,y>0;若点A(2,y1)与点B(3,y2)在该直线上,则y1y2(填“>”,“<”或“=”)
(3)、坐标原点到该直线的距离为 .22. 如图,长方形纸片ABCD中,AB=8,BC=10,折叠纸片的一边AD,使点D落在BC边上的点F处,AE为折痕,请回答下列问题: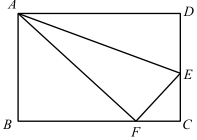 (1)、求线段DE的长度;(2)、若点P为线段AE上的一个动点,连接BP和FP,则线段BP+FP的最小值是 .23. 2019年4月,第二届“一带一路”国际合作高峰论坛在北京举行,共签署了总额640多亿美元的项目合作协议.某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.(1)、甲种商品与乙种商品的销售单价各是多少元?(2)、设甲、乙两种商品的销售总收入为W万元,销售甲种商品m万件,
(1)、求线段DE的长度;(2)、若点P为线段AE上的一个动点,连接BP和FP,则线段BP+FP的最小值是 .23. 2019年4月,第二届“一带一路”国际合作高峰论坛在北京举行,共签署了总额640多亿美元的项目合作协议.某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区,已知2件甲种商品与3件乙商品的销售收入相同,3件甲种商品比2件乙种商品的销售收入多1500元.(1)、甲种商品与乙种商品的销售单价各是多少元?(2)、设甲、乙两种商品的销售总收入为W万元,销售甲种商品m万件,①用含m的式子表示W;
②若甲、乙两种商品的销售收入为5400万元,则销售甲种商品多少万件?
24. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示. (1)、根据图象,求出y1、y2关于x的函数关系式;(2)、设两车之间的距离为S千米,求两车相遇前S关于x的函数关系式;(3)、甲、乙两地间有A、B两个加油站,相距200千米,A加油站在甲地与B加油站之间,若两车相遇后,客车进入B加油站时,出租车恰好进入A加油站,求此时两车的行驶时间x的值和A加油站到甲地的距离.25. 如图1,平面直角坐标系中,直线y=﹣x+m交x轴于点A(4,0),交y轴正半轴于点B,直线AC交y轴负半轴于点C,且BC=AB.
(1)、根据图象,求出y1、y2关于x的函数关系式;(2)、设两车之间的距离为S千米,求两车相遇前S关于x的函数关系式;(3)、甲、乙两地间有A、B两个加油站,相距200千米,A加油站在甲地与B加油站之间,若两车相遇后,客车进入B加油站时,出租车恰好进入A加油站,求此时两车的行驶时间x的值和A加油站到甲地的距离.25. 如图1,平面直角坐标系中,直线y=﹣x+m交x轴于点A(4,0),交y轴正半轴于点B,直线AC交y轴负半轴于点C,且BC=AB. (1)求线段AC的长度.(1)、P为线段AB(不含A,B两点)上一动点.
(1)求线段AC的长度.(1)、P为线段AB(不含A,B两点)上一动点.①如图2,过点P作y轴的平行线交线段AC于点Q,记四边形APOQ的面积为S,点P的横坐标为t,当S=时,求t的值.
②M为线段BA延长线上一点,且AM=BP,在直线AC上是否存在点N,使得△PMN是以PM为直角边的等腰直角三角形?若存在,直接写出点N的坐标;若不存在,请说明理由.