北京市房山区燕山地区2021-2022学年八年级上学期期中数学试题
试卷更新日期:2022-09-13 类型:期中考试
一、单选题
-
1. 下列各组图形中,是全等图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算结果正确的是A、 B、 C、 D、3. 计算28x4y2÷(-7x3y)的正确结果是( )A、4xy2 B、4xy C、-4xy2 D、-4xy4. 八边形的内角和等于( )A、900° B、1080° C、1260° D、1440°5. 如图,要测量湖两岸相对两点A,B的距离,可以在AB的垂线BF上取两点C,D,使CD=BC,再在BF的垂线DG上取点E,使点A,C,E在一条直线上,可得 . 判定全等的依据是( )
2. 下列运算结果正确的是A、 B、 C、 D、3. 计算28x4y2÷(-7x3y)的正确结果是( )A、4xy2 B、4xy C、-4xy2 D、-4xy4. 八边形的内角和等于( )A、900° B、1080° C、1260° D、1440°5. 如图,要测量湖两岸相对两点A,B的距离,可以在AB的垂线BF上取两点C,D,使CD=BC,再在BF的垂线DG上取点E,使点A,C,E在一条直线上,可得 . 判定全等的依据是( )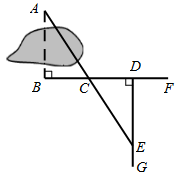 A、 B、 C、 D、6. 如图所示,在下列条件中,不能判断 ≌ 的条件是( )
A、 B、 C、 D、6. 如图所示,在下列条件中,不能判断 ≌ 的条件是( ) A、 , B、 , C、 , D、 ,7. 一副三角板按如图所示方式叠放在一起,则图中∠等于( )
A、 , B、 , C、 , D、 ,7. 一副三角板按如图所示方式叠放在一起,则图中∠等于( )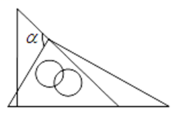 A、105° B、115° C、120° D、125°8. 如图,从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形,然后拼成一个平行四边形,那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )
A、105° B、115° C、120° D、125°8. 如图,从边长为a的大正方形纸板中挖去一个边长为b的小正方形后,将其裁成四个相同的等腰梯形,然后拼成一个平行四边形,那么通过计算两个图形阴影部分的面积,可以验证成立的公式为( )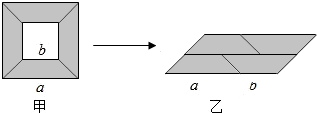 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9.
如图,把手机放在一个支架上面,就可以非常方便地使用,这是因为手机支架利用了三角形的 性.
 10. 计算: .11. 如图,在△ABC中,D是AC延长线上一点,∠A=50°,∠B=70°,则∠BCD=°.
10. 计算: .11. 如图,在△ABC中,D是AC延长线上一点,∠A=50°,∠B=70°,则∠BCD=°. 12. (-18a2b+10b2)÷(-2b)=-18a2b÷+10b2÷(-2b)= .13. 如图,△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,则点D到AB的距离等于cm.
12. (-18a2b+10b2)÷(-2b)=-18a2b÷+10b2÷(-2b)= .13. 如图,△ABC中,∠C=90°,AD平分∠BAC,CD=3cm,则点D到AB的距离等于cm.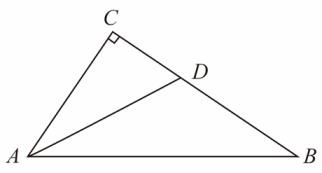 14. 已知三角形的两边长分别为3和7,第三边为x,则x的取值范围是 .15. 小区中一块绿地的形状如图中阴影部分所示,则其面积为 . (用含字母a,b,m的代数式表示)
14. 已知三角形的两边长分别为3和7,第三边为x,则x的取值范围是 .15. 小区中一块绿地的形状如图中阴影部分所示,则其面积为 . (用含字母a,b,m的代数式表示)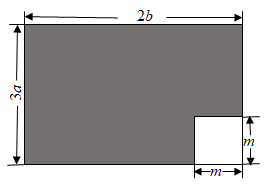 16. 如图,在△中, , 和的平分线交于点 , 得;和的平分线交于点 , 得;和的平分线交于点 , 则 .
16. 如图,在△中, , 和的平分线交于点 , 得;和的平分线交于点 , 得;和的平分线交于点 , 则 .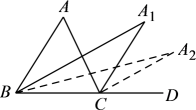
三、解答题
-
17. 计算:(1)、 ;(2)、 ;(3)、 ;(4)、 .18. 按要求画图.
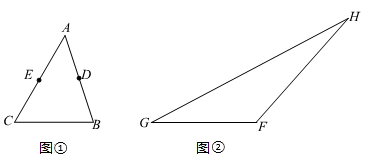 (1)、如图①,在△ABC中,点D,E分别是AB,AC的中点,画出△ABC的中线AT;(2)、如图②,在△FGH中,画出边GH的高FM,边GF的高HN.19. 下面是“作一个角等于已知角”的尺规作图过程.
(1)、如图①,在△ABC中,点D,E分别是AB,AC的中点,画出△ABC的中线AT;(2)、如图②,在△FGH中,画出边GH的高FM,边GF的高HN.19. 下面是“作一个角等于已知角”的尺规作图过程.已知:∠AOB.
求作:∠A′O′B′,使∠A′O′B′=∠AOB.
作法:如图,
①画射线O′A′;
②以O为圆心,任意长为半径画弧,交OA于点M,交OB于点N;
③以O′为圆心,OM长为半径画弧,交O′A′于点M′;
④以M′为圆心,MN长为半径画弧,交前弧于点N′;
⑤过N′作射线O′B′,则∠A′O′B′即为所求.
根据上述尺规作图过程,
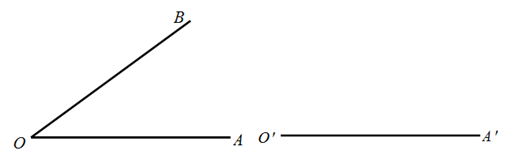 (1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的推理.
(1)、使用直尺和圆规,补全图形;(保留作图痕迹)(2)、完成下面的推理.∵作图步骤③中,以O′为圆心,OM长为半径画弧,交O′A′于点M′,
∴OM= ▲ .
又∵作图步骤④中,以M′为圆心,MN长为半径画弧,交前弧于点N′,
∴ON= ▲ , MN= ▲ ,
∴△MON≌△M′O′N′, ( )(填推理的依据)
∴∠A′O′B′=∠AOB.
20. 求出下列图形中的值.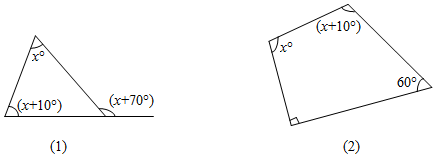 21. 化简求值: , 其中 .22. 已知x2-2x=3,求代数式x(x-4)+(x-3)(x+3)的值23. 如图,已知:AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
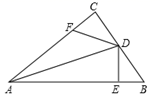
21. 化简求值: , 其中 .22. 已知x2-2x=3,求代数式x(x-4)+(x-3)(x+3)的值23. 如图,已知:AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C. 24. 在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,BD=DF.
24. 在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于点E,点F在AC上,BD=DF.求证:CF=EB
 25. 如图, , 垂足分别为D,E, . 求的长.
25. 如图, , 垂足分别为D,E, . 求的长.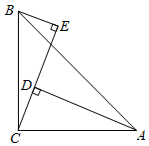 26. 阅读,学习和解题.(1)、阅读和学习下面的材料:
26. 阅读,学习和解题.(1)、阅读和学习下面的材料:比较355 , 444 , 533的大小.
分析:小刚同学发现55,44,33都是11的倍数,于是把这三个数都转化为指数为11的幂,然后通过比较底数的方法,比较了这三个数的大小.解法如下:
解:∵ , , ,
∴ .
学习以上解题思路和方法,然后完成下题:
比较34040 , 43030 , 52020的大小.
(2)、阅读和学习下面的材料:已知am=3,an=5,求a3m+2n的值.
分析:小刚同学发现,这些已知的和所求的幂的底数都相同,于是逆用同底数幂和幂的乘方的公式,完成题目的解答.解法如下:
解:∵=34=27,==32=25,
∴=27×25=675.
学习以上解题思路和方法,然后完成下题:
已知am=2,an=3,求a2m+3n的值.
(3)、计算:(-16)505×(-0.5)2021 .27. 已知,△ABC中,∠C>∠B,AE平分∠BAC,M是AE上一点,MN⊥BC于N.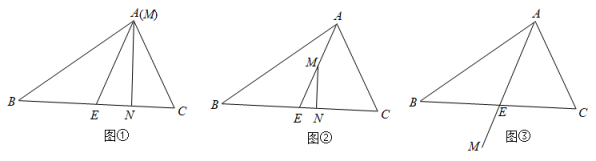 (1)、如图①,当点M与A重合时,若∠B=40°,∠C=80°,求∠EMN的度数;(2)、如图②,当点M在线段AE上(不与A,E重合),用等式表示∠EMN与∠B,∠C之间的数量关系,并证明你的结论;(3)、如图③,当点M在线段AE的延长线上,连接MC,过点A做MC的垂线,交MC的延长线于点F,交BC的延长线上于点D.
(1)、如图①,当点M与A重合时,若∠B=40°,∠C=80°,求∠EMN的度数;(2)、如图②,当点M在线段AE上(不与A,E重合),用等式表示∠EMN与∠B,∠C之间的数量关系,并证明你的结论;(3)、如图③,当点M在线段AE的延长线上,连接MC,过点A做MC的垂线,交MC的延长线于点F,交BC的延长线上于点D.①依题意补全图形;
②若∠B=α°,∠ACB=β°,∠D=γ°,则∠AMC=°.
(用含α,β,γ的式子表示)