安徽省淮南市田家庵区2021-2022学年八年级上学期期中考试数学试题
试卷更新日期：2022-09-13 类型：期中考试
一、单选题
-
1. 下面四个美术字中可以看作轴对称图形的是（ ）A、
B、
C、
D、
2. 如果一个三角形的两边长分别为5cm和8cm，则第三边长可能是（ ）A、2cm B、3cm C、12cm D、13cm3. 已知一个多边形的内角和是其外角和的3倍，则这个多边形的边数是（ ）A、6 B、7 C、9 D、84. 在下列条件中：①∠A+∠B=∠C，②∠A：∠B：∠C=1：2：3，③∠A=90°﹣∠B，④∠A=∠B= ∠C中，能确定△ABC是直角三角形的条件有（ ）A、1个 B、2个 C、3个 D、4个5. 下列条件中，能判定△ABC≌△DEF的是（ ）A、∠A＝∠D，∠B＝∠E，AC＝DF B、∠A＝∠E，AB＝EF，∠B＝∠D C、∠A＝∠D，∠B＝∠E，∠C＝∠F D、AB＝DE，BC＝EF，∠A＝∠E6. 如图，把一张矩形纸片ABCD沿对角线AC折叠，点B的对应点为B′，AB′与DC相交于点E，则下列结论一定正确的是（ ）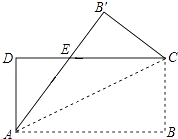
A、∠DAB′=∠CAB′ B、∠ACD=∠B′CD C、AD=AE D、AE=CE7. 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE＝DG，△ADG和△AED的面积分别为50和38，则△EDF的面积为（ ）
A、6 B、10 C、12 D、228. 如图，在△ABC中，AB＝AC，点E，F是中线AD上的两点，则图中可证明为全等三角形的有（ ）
A、3对 B、4对 C、5对 D、6对9. 如图，在△ABC中，∠ACB=100°，AC=AE，BC=BD，则∠DCE的度数为（ ）.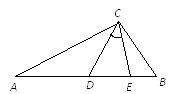
A、20° B、25° C、30° D、40°10. 如图，在△ABC中，∠A为钝角，AB=20cm，AC=12cm，点P从点B出发以3cm/s的速度向点A运动，点Q同时从点A出发以2cm/s的速度向点C运动，其中一个动点到达端点时，另一个动点也随之停止运动.当△APQ是等腰三角形时，运动的时间是（ ）
A、2.5s B、3s C、3.5s D、4s二、填空题
-
11. 已知等腰三角形的周长为15cm，其中一边长为7 cm，则底边长为.
12. 已知点A（1，3）和B（1，－3），则点A，B关于对称．13. 已知a，b，c是△ABC的三边，化简：|a＋b－c|＋|b－a－c|＝ ．14. 在平面直角坐标系中，已知点 ， 点Q在y轴上，是等腰三角形，则满足条件的点Q共有个．
15. 如图，在Rt△ABC中，∠B＝90°，AB＝3cm，S△ABC＝6cm2 ， 将△ABC折叠，使点C与点A重合，得折痕DE，则△ABE的周长等于cm.
16. 如图，在△ABC中，AD是BC边上的中线，BE是△ABD中AD边上的中线，若△ABC的面积是80，则△ABE的面积是 ．
17. 如图，在 中， ， ，点C的坐标为 ，点A的坐标为 ，则B点的坐标是.
18. 如图，已知∠AOB＝α，在射线OA、OB上分别取点OA1＝OB1 ， 连接A1B1 ， 在B1A1、B1B上分别取点A2、B2 ， 使B1B2＝B1A2 ， 连接A2B2…按此规律上去，记∠A2B1B2＝θ1 ， ∠A3B2B3＝θ2 ， …，∠An＋1BnBn＋1＝θn，则θn＝ ．
三、解答题
-
19. 如图，某地有两所大学和两条相交叉的公路，（点M，N表示大学，AO，BO表示公路），现计划在∠AOB内部修建一座物资仓库，希望仓库到两所大学的距离相等，到两条公路的距离也相等，你能确定仓库P应该建在什么位置吗？在所给的图形中画出你的设计方案．
20. 在△ABC中，BO、CO分别平分∠CBA、∠BCA，求证：∠COB= ∠CAB+90°．
21. 如图，在∠AOB的两边OA，OB上分别取OM＝ON，∠OME＝∠OND，DN和EM相交于点C，CD＝CE．求证：点C在∠AOB的平分线上．
