陕西省2022届高三上学期理数元月联考试卷
试卷更新日期:2022-09-13 类型:期末考试
一、单选题
-
1. 已知集合 , , 则( )A、(1,4) B、(1,2) C、 D、2. 已知复数的实部与虚部的和为12,则( )A、3 B、4 C、5 D、63. 北京天坛圜丘坛的地面由石板铺成,最中间的是圆形的天心石,围绕天心石的是9圈扇环形的石板,从内到外各圈的石板数依次为 , 设数列为等差数列,它的前项和为 , 且 , , 则( )
 A、189 B、252 C、324 D、4054. 已知为抛物线上一点,点到的焦点的距离为7,到轴的距离为5,则( )A、3 B、4 C、5 D、65. 某几何体的三视图如图所示,则该几何体的体积是( )
A、189 B、252 C、324 D、4054. 已知为抛物线上一点,点到的焦点的距离为7,到轴的距离为5,则( )A、3 B、4 C、5 D、65. 某几何体的三视图如图所示,则该几何体的体积是( ) A、18 B、36 C、54 D、1086. 已知 , , , 则( )A、 B、 C、 D、7. 江西景德镇青花瓷始创于元代,到明清两代达到了顶峰,它蓝白相映怡然成趣,晶莹明快,美观隽永.现有某青花瓷花瓶的外形可看成是焦点在轴上的双曲线的一部分绕其虚轴旋转所形成的曲面,如图所示,若该花瓶的瓶身最小的直径是4,瓶口和底面的直径都是8,瓶高是6,则该双曲线的标准方程是( )
A、18 B、36 C、54 D、1086. 已知 , , , 则( )A、 B、 C、 D、7. 江西景德镇青花瓷始创于元代,到明清两代达到了顶峰,它蓝白相映怡然成趣,晶莹明快,美观隽永.现有某青花瓷花瓶的外形可看成是焦点在轴上的双曲线的一部分绕其虚轴旋转所形成的曲面,如图所示,若该花瓶的瓶身最小的直径是4,瓶口和底面的直径都是8,瓶高是6,则该双曲线的标准方程是( ) A、 B、 C、 D、8. 已知函数 , 则下列结论正确的是( ).A、的最小正周期是 B、的图象关于点对称 C、在上单调递增 D、是奇函数9. 已知函数恰有4个零点,则a的取值范围是( ).A、 B、 C、 D、10. 在四边形中(如图1所示), , , , 将四边形沿对角线折成四面体(如图2所示),使得 , E,F,G分别为棱 , , 的中点,连接 , , 则下列结论错误的是( ).
A、 B、 C、 D、8. 已知函数 , 则下列结论正确的是( ).A、的最小正周期是 B、的图象关于点对称 C、在上单调递增 D、是奇函数9. 已知函数恰有4个零点,则a的取值范围是( ).A、 B、 C、 D、10. 在四边形中(如图1所示), , , , 将四边形沿对角线折成四面体(如图2所示),使得 , E,F,G分别为棱 , , 的中点,连接 , , 则下列结论错误的是( ). A、 B、直线与所成角的余弦值为 C、C,E,F,G四点不共面 D、四面体外接球的表面积为11. 已知 , 数列1,1,2,1,1,2,4,2,1,1,2,4,8,4,2,1,···,1,2,4,···, , , ···,2,1,···的前项和为 , 若 , 则的最小值为( )A、81 B、90 C、100 D、2021
A、 B、直线与所成角的余弦值为 C、C,E,F,G四点不共面 D、四面体外接球的表面积为11. 已知 , 数列1,1,2,1,1,2,4,2,1,1,2,4,8,4,2,1,···,1,2,4,···, , , ···,2,1,···的前项和为 , 若 , 则的最小值为( )A、81 B、90 C、100 D、2021二、多选题
-
12. 随着互联网的飞速发展,网上购物已成为了流行的消费方式.某网店第三季度的服装产品的销售总额和其中某款服装的销售额占当月服装产品销售总额的百分比如图所示:

下列结论错误的是( )
A、该款服装这3个月的销售额逐月递减 B、该款服装这3个月的销售总额为23.69万元 C、该款服装8月份和9月份的销售额相同 D、该款服装8月份和9月份的销售总额大于7月份的销售额三、填空题
-
13. 已知向量 , , 且 , 则.14. 的展开式中的系数是 . (用数字作答)15. 若 , 满足约束条件则的最大值为 .16. 若曲线在点处的切线与曲线相切,则 .
四、解答题
-
17. 在中,内角A,B,C所对的边分别为a,b,c,的面积为S,已知 , .(1)、求a;(2)、若 , 求A.18. 某部门为了解某企业在生产过程中的用电情况,对其每天的用电量做了记录,得到了大量该企业的日用电量(单位:度)的统计数据,从这些数据中随机抽取15天的数据作为样本,得到如图所示的茎叶图.若日用电量不低于200度,则称这一天的用电量超标.
 (1)、从这15天中随机抽取4天,求抽取的4天中至少有3天的日用电量超标的概率;(2)、从这15天的样本数据中随机抽取4天的日用电量数据,记这4天中日用电量超标的天数为X,求X的分布列和数学期望.19. 如图,是圆的直径,圆所在的平面,为圆周上一点,为线段的中点, , .
(1)、从这15天中随机抽取4天,求抽取的4天中至少有3天的日用电量超标的概率;(2)、从这15天的样本数据中随机抽取4天的日用电量数据,记这4天中日用电量超标的天数为X,求X的分布列和数学期望.19. 如图,是圆的直径,圆所在的平面,为圆周上一点,为线段的中点, , .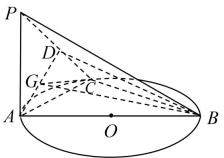 (1)、证明:平面平面.(2)、若为的中点,求二面角的余弦值.20. 已知椭圆的左,右顶点分别是 , , 且 , 是椭圆上异于 , 的不同的两点.(1)、若 , 证明:直线必过坐标原点;(2)、设点是以为直径的圆和以为直径的圆的另一个交点,记线段的中点为 , 若 , 求动点的轨迹方程.
(1)、证明:平面平面.(2)、若为的中点,求二面角的余弦值.20. 已知椭圆的左,右顶点分别是 , , 且 , 是椭圆上异于 , 的不同的两点.(1)、若 , 证明:直线必过坐标原点;(2)、设点是以为直径的圆和以为直径的圆的另一个交点,记线段的中点为 , 若 , 求动点的轨迹方程.
-